今回は点Pの存在範囲を示すとき, ![]() の範囲が少々複雑な場合を書いておきます。
の範囲が少々複雑な場合を書いておきます。
【例】△OABにおいて, 次の式を満たす点Pの存在範囲を求めよ。![]() ,
, ![]() ,
, ![]()
【解法】先ず, ![]() の範囲において, 2つの不等式に分割する。
の範囲において, 2つの不等式に分割する。![]() は
は![]() かつ
かつ![]() であるから, この2つの不等式で分けて考える。
であるから, この2つの不等式で分けて考える。![]() のとき,
のとき,![]()
となるので, このときのPの存在範囲は, 次の図の色を付けた部分になる(境界線は含む)。ただし, A![]() は
は![]() の中点である。
の中点である。
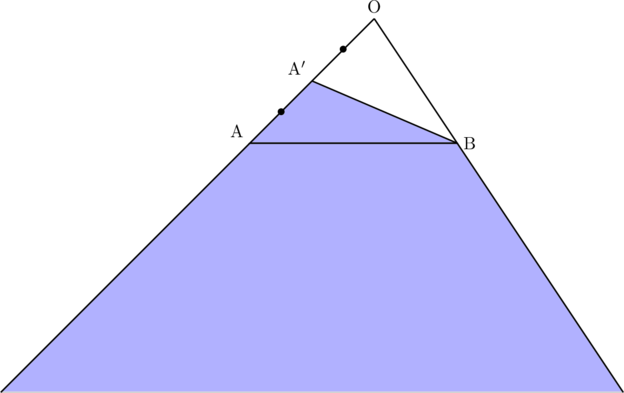
次に
となるので, このときPの存在範囲は, 次の図の色を付けた部分になる(境界線は含む)。ただし,
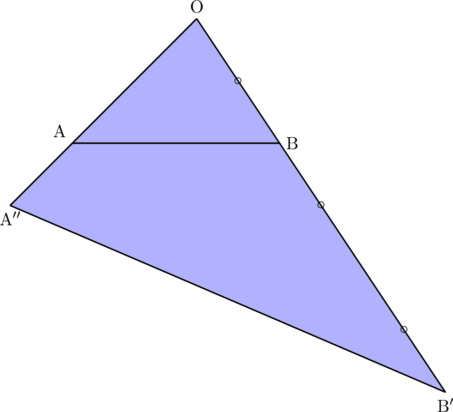
以上より求める範囲は
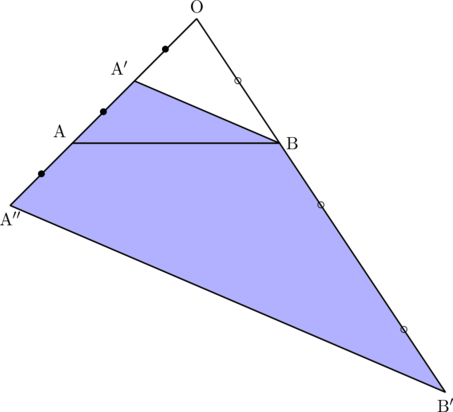
攻略ポイント
不等式を2つに分割して考えて, 共通部分を図示する。
 TikZ:高校数学:ベクトルと点Pの存在範囲1
TikZ:高校数学:ベクトルと点Pの存在範囲1 数樂管理人のブログ
数樂管理人のブログ 

