こんにちは。今回は絶対値を含む関数の積分です。それではいきましょう。
絶対値を含む関数の面積
【問題】![]() の値を求めよ。
の値を求めよ。
【解答】![]()
![]() ,
, ![]() のとき,
のとき, ![]()
![]() のとき,
のとき, ![]()
となり, それぞれグラフを描くと下の図のようになり, 求めるのは色のついた部分。
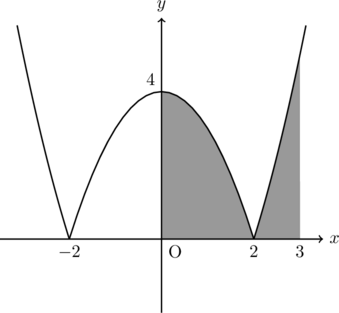
したがって,
![Rendered by QuickLaTeX.com \begin{array}{lll}&&\displaystyle\int^3_0\left|x^2-4\right|\,dx\\&=&\displaystyle\int^2_0(-x^2+4)\,dx+\displaystyle\int^3_2(x^2-4)\,dx\\&=&\left[-\dfrac{x^3}{3}+4x\right]^2_0+\left[\dfrac{x^3}{3}-4x\right]^3_2\\ &=&\left(-\dfrac83+8\right)+\left\{\left(9-12\right)-\left(\dfrac83-8\right)\right\}\\&=&\dfrac{23}{3}\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-4733cd2312ed061649e9d85cedb07c3a_l3.png)
こんにちは。今回は絶対値を含む関数の積分です。それではいきましょう。
絶対値を含む関数の面積
【問題】![]() の値を求めよ。
の値を求めよ。
【解答】![]()
![]() ,
, ![]() のとき,
のとき, ![]()
![]() のとき,
のとき, ![]()
となり, それぞれグラフを描くと下の図のようになり, 求めるのは色のついた部分。

![Rendered by QuickLaTeX.com \begin{array}{lll}&&\displaystyle\int^3_0\left|x^2-4\right|\,dx\\&=&\displaystyle\int^2_0(-x^2+4)\,dx+\displaystyle\int^3_2(x^2-4)\,dx\\&=&\left[-\dfrac{x^3}{3}+4x\right]^2_0+\left[\dfrac{x^3}{3}-4x\right]^3_2\\ &=&\left(-\dfrac83+8\right)+\left\{\left(9-12\right)-\left(\dfrac83-8\right)\right\}\\&=&\dfrac{23}{3}\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-4733cd2312ed061649e9d85cedb07c3a_l3.png)