こんにちは。今回は定期テストはもちろん, それ以外でも頻出の問題をやってみましょう。実際に問題を解いてみてください。解法はそれから見てください。
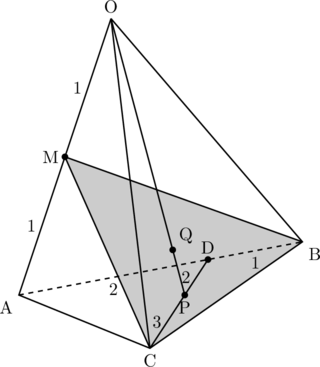
【問題】四面体OABCにおいて, 辺ABを2 : 1に内分する点をD, 線分CDを3 : 2に内分する点をP, 辺OAの中点をMとする。また, OPと△MBCとの交点をQとする。![]() ,
, ![]() ,
, ![]() とするとき, 次の問いに答よ。
とするとき, 次の問いに答よ。
(1) ![]() を
を![]() ,
, ![]() ,
, ![]() を用いて表せ。
を用いて表せ。
(2) ![]() を
を![]() ,
, ![]() ,
, ![]() を用いて表せ。
を用いて表せ。
(3) ![]() を求めよ。
を求めよ。
【解答】
(1)
よって,
(2) O, Q, Pは一直線上にあるので,
とおける。
したがって,
となる。
4点M, B, C, Qは同一平面上にあるから,
と表せる。
ここで,
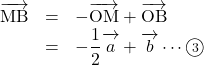
また,
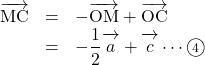
ここで,
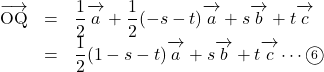
4点O, A, B, Cは同一平面上にないので,
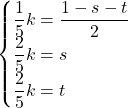
これを解いて,
よって,
(3) (2)より,
これより, OQ : OP
したがって, OQ : QP
ここがポイント
所定のベクトルを2通りの表し方で表して, 連立方程式を解いて求める。
 数樂管理人のブログ
数樂管理人のブログ 


