TikZ：高校数学：積分：面積の値が一定になることの証明

2021年12月31日2022年4月25日

こんにちは。今回は面積の値が一定になることの証明問題をやってみましょう。それではどうぞ。

面積の値が一定になることを示す問題

【問題】放物線 $y=x^2+1$ 上の点 $( a, b )$ における放物線の接線と放物線 $y=x^2$ で囲まれた図形の面積は, $a$ の値に関係なく一定であることを示せ。

【解答】 $y=x^2+1\cdots\maru1$ を $x$ について微分すると, $y'=2x$
点 $( a, b )$ は $\maru1$ 上にあるので, $b=a^2+1$ が成り立ち.
点 $( a, b )$ は, 点 $( a, a^2+1 )$ と書ける。これを点Pとする。
したがって, この点Pにおける接線の方程式は,
$y=2a(x-a)+a^2+1$ とおけ,
$y=2ax-a^2+1\cdots\maru2$ となる。
この直線と $y=x^2\cdots\maru3$ の交点の $x$ 座標を求めると,
$x^2=2ax-a^2+1$
$x^2-2ax+a^2=1$
$(x-a)^2=1$
$x-a=\pm1$
$x=a\pm1$ となる。
この様子を図示すると, 以下のようになる。

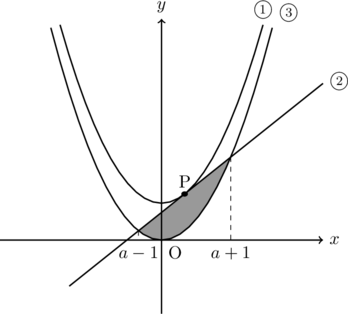
したがって, 求める面積は,
$\begin{array}{lll}&&\displaystyle\int^{a+1}_{a-1}\left(2ax-a^2+1-x^2\right)\,dx\\&=&-\displaystyle\int^{a+1}_{a-1}(x-a-1)(x-a+1)\,dx\\&=&\dfrac{\left\{(a+1)-(a-1)\right\}^3}{6}\\&=&\dfrac43\end{array}$
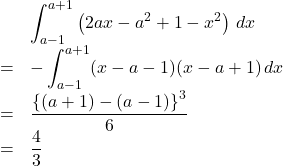
よって, $a$ の値に関係なく面積が一定であることが示せた。

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル