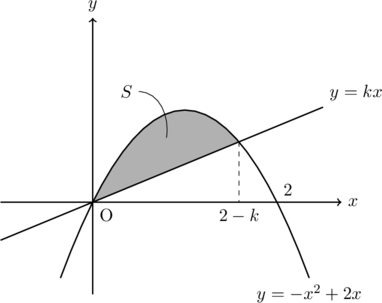
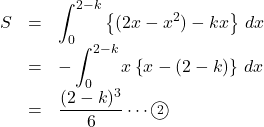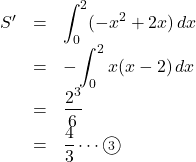こんにちは。今回は放物線と![]() 軸に囲まれた面積の二等分線について考えていきましょう。
軸に囲まれた面積の二等分線について考えていきましょう。
【問題】直線![]() が, 放物線
が, 放物線![]() と
と![]() 軸で囲まれた図形の面積を2等分するように, 定数
軸で囲まれた図形の面積を2等分するように, 定数![]() の値を定めよ。
の値を定めよ。
【解答】放物線![]() と直線
と直線![]() で囲まれた部分の面積を
で囲まれた部分の面積を![]() とする。
とする。
2つのグラフの交点を求めると, ![]()
![]()
![]()
![]()
面積を2等分するためには, ![]() であることが条件,
であることが条件,
これより, ![]()
ここで,
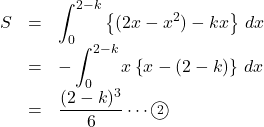
放物線と
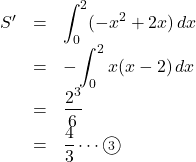
これは
こんにちは。今回は放物線と![]() 軸に囲まれた面積の二等分線について考えていきましょう。
軸に囲まれた面積の二等分線について考えていきましょう。
【問題】直線![]() が, 放物線
が, 放物線![]() と
と![]() 軸で囲まれた図形の面積を2等分するように, 定数
軸で囲まれた図形の面積を2等分するように, 定数![]() の値を定めよ。
の値を定めよ。
【解答】放物線![]() と直線
と直線![]() で囲まれた部分の面積を
で囲まれた部分の面積を![]() とする。
とする。
2つのグラフの交点を求めると, ![]()
![]()
![]()
![]()
面積を2等分するためには, ![]() であることが条件,
であることが条件,
これより, ![]()