こんにちは。今回は空間における座標で, 4点が同じ平面上にあるとき, 未知の座標を求めるというもの。例題を見ながらいってみましょう。
【例題】4点A![]() , B
, B![]() , C
, C![]() , D
, D![]() が同じ平面上にあるとき,
が同じ平面上にあるとき, ![]() の値を定めよ。
の値を定めよ。
【方針】4点A, B, C, Dが同じ平面上にあるということは, ![]() となる実数
となる実数![]() が存在することになる。ことを利用して,
が存在することになる。ことを利用して, ![]() の値を求める。
の値を求める。
【解法】 4点A, B, C, Dが同じ平面上にあるということは, ![]() となる実数
となる実数![]() が存在することになる。
が存在することになる。![]() ,
, ![]() ,
, ![]() なので,
なので,
これらを![]() にあてはめると,
にあてはめると, ![]()
これより, 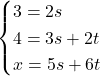
これを解いて, ![]() ,
, ![]() ,
, ![]()
よって, ![]()
ここがポイント
4点A, B, C, Dが同じ平面上にあるということは, ![]() となる実数
となる実数![]() が存在することになる。ことを利用して,
が存在することになる。ことを利用して, ![]() に関する連立方程式をつくり,
に関する連立方程式をつくり, ![]() の値を求める。
の値を求める。
 数樂管理人のブログ
数樂管理人のブログ 

