こんにちは。今回は楕円の外側からの接線の式を2通りの求め方でやってみようと思います。例題を見ながらやっていきましょう。
【例題】点(2, 1)から楕円![]() に引いた接線を求めよ。
に引いた接線を求めよ。
【解法1】接線を![]() とおく。
とおく。
これを楕円の式に代入すると, ![]()
両辺4倍して展開すると, ![]()
![]() について整理すると,
について整理すると, ![]()
これが重解をもつことから, 判別式![]() を用いると,
を用いると, ![]()
![]()
![]()
![]()
よって求める接線の方程式は![]()
【解法2】楕円上の接点を![]() と置き, 接線の方程式を,
と置き, 接線の方程式を, ![]() とおく。
とおく。![]() が点(2, 1)を通るので,
が点(2, 1)を通るので, ![]() と置ける。これを
と置ける。これを![]() について解くと,
について解くと, ![]()
ここで, ![]() は楕円上の点であるから,
は楕円上の点であるから, ![]() が成り立つ。
が成り立つ。![]() に
に![]() を代入すると,
を代入すると, ![]()
展開して, 整理すると, ![]()
これを解いて, ![]()
これと![]() から
から![]() を求めると,
を求めると,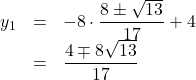
この![]() を
を![]() に代入すると, 求める接線の方程式は,
に代入すると, 求める接線の方程式は, 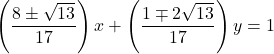
楕円の外からの接線
単純に接線求めるだけなら, Case1, Case2どちらでもいい。
問題に接点を求める場合が含まれるのであればCase2の解き方が有効である。
問題に接点を求める場合が含まれるのであればCase2の解き方が有効である。
 数樂管理人のブログ
数樂管理人のブログ 

