こんにちは。今回は三角形の存在条件について書いておきます。感覚的に2つの辺の和が最大辺より長くないと三角形ができないのは理解できると思います。2辺の和が最大辺とちょうどのときや短いときは三角形ができませんよね。それを深堀していきましょう。
△ABCの3辺![]() において, 次の不等式が成り立つとき, 三角形は存在する。
において, 次の不等式が成り立つとき, 三角形は存在する。![]()
![]() が最大辺なら
が最大辺なら![]()
三角形が存在するということは, 三角形に関する等式で, 実数解が存在することを意味します。今回は余弦定理を用いて, 三角形の存在条件を示していきます。
![]() において,
において, ![]() のとる範囲は,
のとる範囲は, ![]() となる。
となる。![]() における
における![]() を余弦定理から
を余弦定理から![]() に置き換えると,
に置き換えると, ![]()
両辺に![]() をかけて,
をかけて, ![]()
各辺々に![]() を移行して,
を移行して, ![]()
両辺に![]() をかけて並べ替えると,
をかけて並べ替えると, ![]()
因数分解して, ![]()
絶対値をとって2乗を外すと![]()
ただし, ![]() であることから
であることから![]() を得る。
を得る。
また, ![]() の
の![]() より,
より, ![]() となり,
となり, ![]() から,
から, ![]() が得られ,
が得られ, ![]() から,
から, ![]() が得られる。
が得られる。
以上より![]()
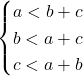
![]() が最大辺なら
が最大辺なら![]() ,
, ![]() は自明,
は自明, ![]() だけで判断できる。
だけで判断できる。
よく使うのは![]() の不等式と
の不等式と![]() が最大辺のとき,
が最大辺のとき, ![]() なので, はじめにこの2つを記した。
なので, はじめにこの2つを記した。
【例題】3辺の長さが次のような三角形は存在するか。
(1) 4, 5, 8
(2) 12, 5, 6
(1) 最大辺は8で, ![]() なので存在する。
なので存在する。
(2) 最大辺は12で, ![]() なので存在しない。
なので存在しない。
三角形の存在条件
△ABCの3辺![]() において, 次の不等式が成り立つとき, 三角形は存在する。
において, 次の不等式が成り立つとき, 三角形は存在する。![]()
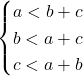
![]() が最大辺なら
が最大辺なら![]() のみでよい。
のみでよい。
 数樂管理人のブログ
数樂管理人のブログ 


