TikZ：中学数学：令和4年度徳島県公立高校入試・数学・大問4　解説

こんにちは。今回は2022年の徳島県の公立高校の入試問題から放物線の問題をやってみようと思います。

放物線の問題

【問題】下の図のように, 関数 $y=ax^2 (a>0)$ のグラフ上に2点A, Bがあり, 点Aの $x$ 座標は $-4$ , 点Bの座標は2である。また, 直線ABと $y$ 軸との交点をCとする。(1)～(3)に答えなさい。

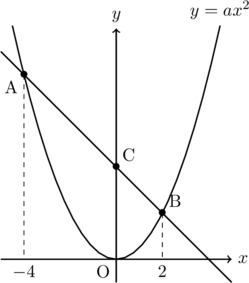
(1) 点Aの $y$ 座標が6のとき, 点Oを回転の中心として, 点Aを点対称移動した点の座標を求めなさい。
(2) $a=\dfrac12$ のとき, 線分ABの長さを求めなさい。
(3) $a=1$ のとき, (a)・(b)に答えなさい。
(a) △OABの面積を求めなさい。
(b) 線分ACの中点をPとし, 点Qを関数 $y=ax^2$ のグラフ上にとる。△OABと△OPQの面積が等しくなるときの点Qの $x$ 座標を求めなさい。ただし, 点Qの $x$ 座標は正とする。
「2022年徳島県公立高校入試」

解答　クリックしてください

(1)点Aの $y$ 座標が6のとき, Aの座標は $(-4, 6)$ である。これを原点Oを中心に180°回転(点対称移動)させることは, 点Aを原点について対称な座標を求めることと等しいので, $x$ 座標, $y$ 座標の符号を変えればよい。したがって, 答えは, $(4, -6)\cdots$ (答)
(2) $a=\dfrac12$ のとき, 放物線の関数は $y=\dfrac12x^2$ となり, 点A, Bの座標はそれぞれ, A $(-4, 8)$ , B $(2, 2)$ となるので, 求める長さは, $\sqrt{(-4-2)^2+(8-2)^2}=\sqrt{72}=6\sqrt{2}$
$6\sqrt2\cdots$ (答)
(3)
(a) $a=1$ のとき, 放物線の関数は $y=x^2$ となり, 点A, Bの座標はそれぞれ, A $(-4, 16)$ , B $(2, 4)$ となり, この2点から直線ABの式は $y=-2x+8$ と分かる。

Rendered by QuickLaTeX.com

求める三角形は $8\times6\times\dfrac12=24\cdots$ (答)
(b) 方針としては, Pの座標を求め, Qの $x$ 座標を文字でおいて, △OPQを文字で表して, それが24になるという方程式をつくる。

Rendered by QuickLaTeX.com

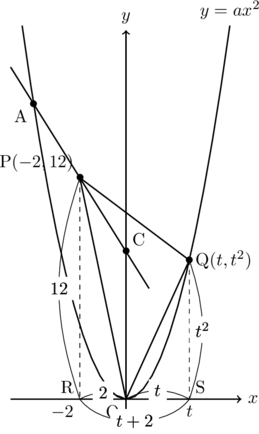
図のように, Pの座標はA $(-4, 16)$ , C $(0, 8)$ だから, Pの座標はその2点の中点だからP $(-2, 12)$ である。
Qの $x$ 座標を $t$ とおくと, Q $(t, t^2)$ と表せる。また, P, Qからそれぞれ $x$ 軸に垂線を下ろし, $x$ 軸との交点をそれぞれR, Sとして, 台形PQSRをつくる。このとき, 上底PR, 下底QSの長さは点P, Qの $y$ 座標になるので, それぞれ, $12, t^2$ となる。また, 台形の高さSRは $t+2$ となるので, 台形の面積は
$(t^2+12)\times(t+2)\times\dfrac12=\dfrac12(t^2+12)(t+2)$ となる。
求める△OPQはこの台形PQSRの面積から△PROと△QSOを引いたものなので,
△PROと△QSOの面積をそれぞれ求めると,
△PRO $=2\times12\times\dfrac12=12$
△QSO $=t\times t^2\times\dfrac12=\dfrac12 t^3$
よって, △OPQは
△OPQ $=\dfrac12(t^2+12)(t+2)-12-\dfrac12 t^3=t^2+6t$
これが24(△OABの面積)になればいいので,
$t^2+6t=24$
$t^2+6t-24=0$
これを解いて, $t=-3\pm\sqrt{33}$
$t>0$ なので, $t=-3+\sqrt{33}$
よって, 求める座標は $-3+\sqrt{33}\cdots$ (答)

放物線の問題

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル