こんにちは。今回は2022年に行われた徳島県の公立高校の入試問題から大問5の平面図形をやってみようと思います。
【問題】図1, 図2のように, AB![]() 4cm,
4cm, ![]() である長方形ABCDを, ある線分を折り目として折り返したものがある。(1)・(2)に答えなさい。
である長方形ABCDを, ある線分を折り目として折り返したものがある。(1)・(2)に答えなさい。
(1) 図1のように, 長方形ABCDを, 辺CD上の点Eと頂点Bを結んだ線分BEを折り目として, 頂点Cが辺AD上にくるように折り返したとき, 頂点Cが移る点をFとする。(a)・(b)に答えなさい。
図1
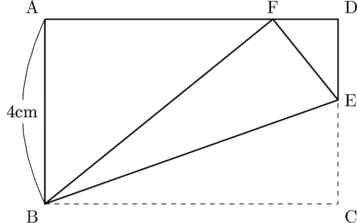
(a)
(b) DE : EC
(2) 図2のように, 長方形ABCDを, 対角線BDを折り目として折り返したとき, 頂点Cが移る点をP, 辺ADと線分BPとの交点をQとする。(a)・(b)に答えなさい。
図2
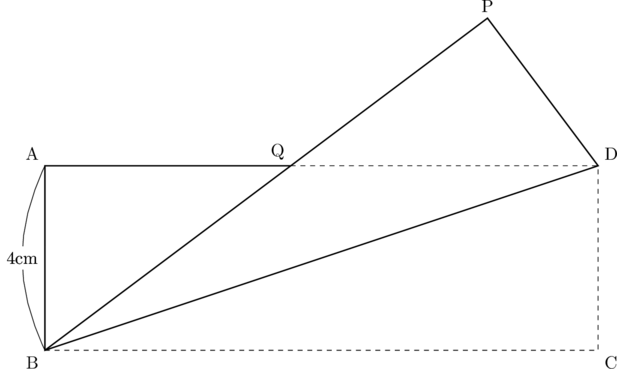
(a) △ABQ
(b) 対角線BDの中点をR, 線分ARと線分BPとの交点をSとする。AD
「2022年徳島県公立高校入試」
(1)(a)
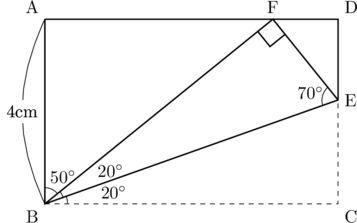
図より
(1)(b)
DE : EC
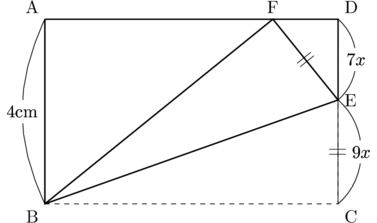
このとき,
したがって, DE
よって, EF
(2)(a)
△ABQと△PDQで,
仮定より,
AB
対頂角は等しいので,
1組の辺とその両端の角がそれぞれ等しいので,
△ABQ
【別解】手間はかかりますが, △QBDが二等辺三角形を示し, QB
(2)(b)
まず最初に線分ARはCの方に延長して, 線分ACとしておきます。理由は△AQS∽△CBSをつくるためです。
次に,
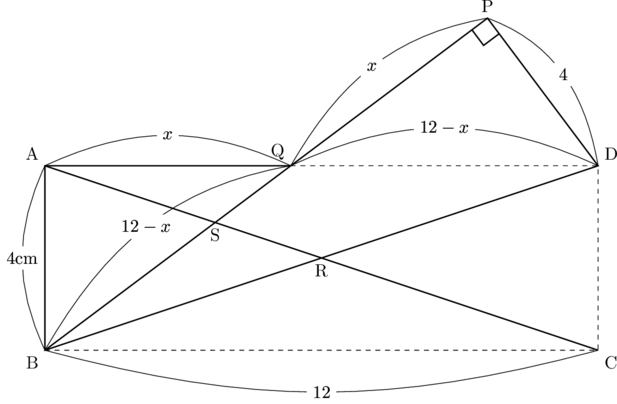
△AQS∽△CBSで相似比は, AQ : CB
したがって, QS : BS
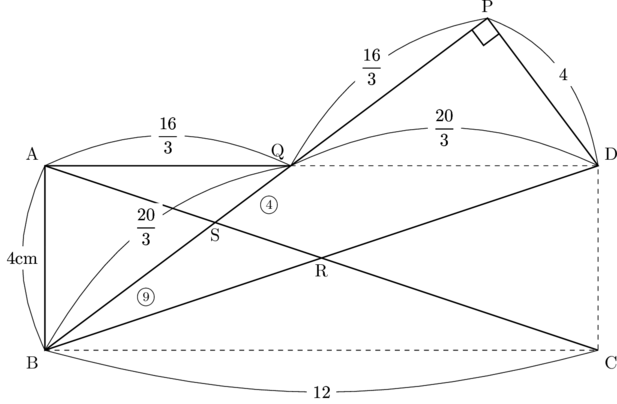
よって,
QS
BS
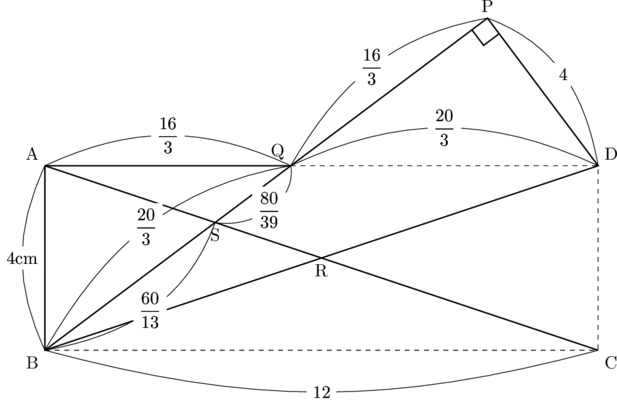
これから, SP
したがって, BS : SP
これから,
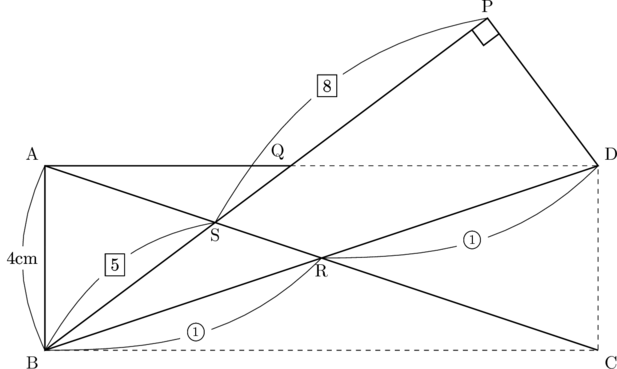
△BRS : △BDP
したがって,
△BRS : 四角形RDPS
よって,
【別解1】△BPD
【別解2】△BPD
【余談】余力のある方はせっかくなんで, (1)でADの長さを求めてみてもいいでしょう。答えは
 数樂管理人のブログ
数樂管理人のブログ 

