こんにちは。今回は複素数平面上で, 異なる3点が同一直線上に並ぶ場合と, 垂直に並ぶ場合ではどのような性質があるのか書いておきます。
複素数平面上の3点![]() ,
, ![]() ,
, ![]() のつくる
のつくる![]() の大きさを考えてみようと思います。同一直線上に並ぶ場合は, この
の大きさを考えてみようと思います。同一直線上に並ぶ場合は, この![]() が
が![]() (
(![]() が
が![]() から見て
から見て![]() と同じ側にあるとき), または,
と同じ側にあるとき), または, ![]() (
(![]() が
が![]() から見て
から見て![]() と反対側にあるとき)になることが考えられます。
と反対側にあるとき)になることが考えられます。
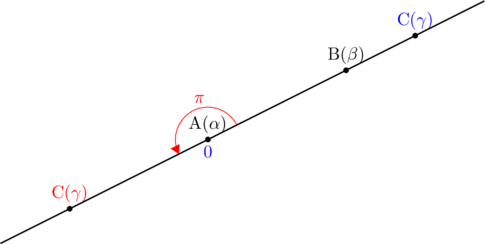
このとき,
となりともに実数になります。
つまり, 3点が同一直線上にある場合,
※2直線のなす角についてはこちらの記事を参照ください。
垂直に交わる場合も, 複素数平面上の3点![]() ,
, ![]() ,
, ![]() のつくる
のつくる![]() の大きさを考えてみようと思います。垂直に交わる場合は, この
の大きさを考えてみようと思います。垂直に交わる場合は, この![]() が
が![]() , または
, または![]() になることが考えられます。
になることが考えられます。
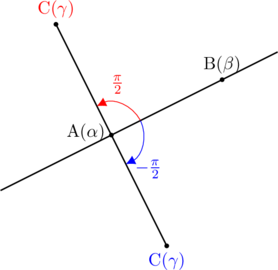
このとき,
となりともに実数部のない純虚数になります。
つまり, 2直線が垂直に交わる場合,
※2直線のなす角についてはこちらの記事を参照ください。
![]() は実数とする。複素数平面上の4点
は実数とする。複素数平面上の4点![]() ,
, ![]() ,
, ![]() ,
, ![]() について, 次の問いに答よ。
について, 次の問いに答よ。![]() 3点
3点![]() ,
, ![]() ,
, ![]() が一直線上にあるとき,
が一直線上にあるとき, ![]() の値を求めよ。
の値を求めよ。![]() 2直線
2直線![]() ,
, ![]() が垂直に交わるとき,
が垂直に交わるとき, ![]() の値を求めよ。
の値を求めよ。
![]() ,
, ![]() ,
, ![]() ,
, ![]() とする。
とする。![]() 3点
3点![]() ,
, ![]() ,
, ![]() が一直線上にあるとき,
が一直線上にあるとき,![]() が実数なので,
が実数なので, 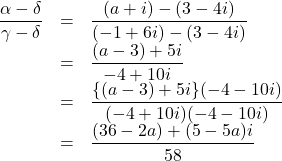
虚数部は0になるので, ![]()
よって, ![]()
![]() 2直線
2直線![]() ,
, ![]() が垂直に交わるとき,
が垂直に交わるとき,![]() が純虚数なので,
が純虚数なので, 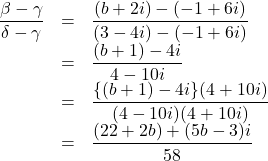
実数部は0になるので, ![]()
よって, ![]()
 TikZ:高校数学:複素数・2直線のなす角と求め方
TikZ:高校数学:複素数・2直線のなす角と求め方 数樂管理人のブログ
数樂管理人のブログ 
