こんにちは。今回は複素数平面上で, 2直線のなす角を求めていきます。
複素数平面上の3点![]() ,
, ![]() ,
, ![]() のつくる
のつくる![]() の大きさを考えてみようと思います。
の大きさを考えてみようと思います。
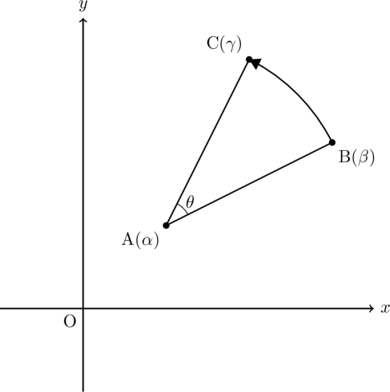
今, 点
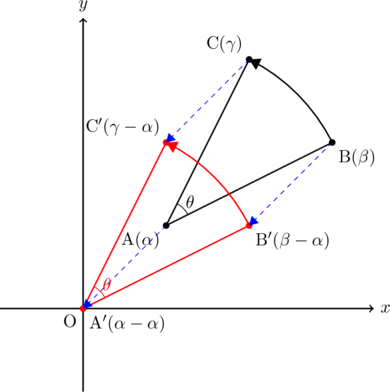
このとき, 点
この式の両辺を
となり,
したがって,
【問】複素数平面上の3点, ![]() ,
, ![]() ,
, ![]() について,
について, ![]() の大きさを求めよ。
の大きさを求めよ。
![]() ,
, ![]() ,
, ![]() とするとき,
とするとき, 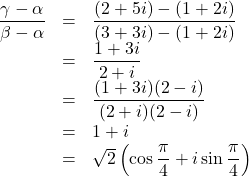
よって, ![]()
 TikZ:高校数学:複素数・同一直線に並ぶ, 垂直に交わるときの性質
TikZ:高校数学:複素数・同一直線に並ぶ, 垂直に交わるときの性質こんにちは。今回は複素数平面上で, 2直線のなす角を求めていきます。
複素数平面上の3点![]() ,
, ![]() ,
, ![]() のつくる
のつくる![]() の大きさを考えてみようと思います。
の大きさを考えてみようと思います。


【問】複素数平面上の3点, ![]() ,
, ![]() ,
, ![]() について,
について, ![]() の大きさを求めよ。
の大きさを求めよ。
![]() ,
, ![]() ,
, ![]() とするとき,
とするとき, 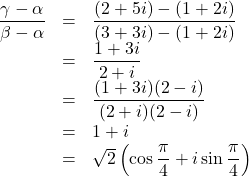
よって, ![]()
 TikZ:高校数学:複素数・同一直線に並ぶ, 垂直に交わるときの性質
TikZ:高校数学:複素数・同一直線に並ぶ, 垂直に交わるときの性質