こんにちは。連続と微分可能について書いておきます。
連続とはグラフがつながっていることです。
関数![]() が
が![]() で連続(つながっている)ということは,
で連続(つながっている)ということは, ![]()
が成り立つことである。
これは, 右側極限の![]() と, 左側極限の
と, 左側極限の![]() が存在し,
が存在し, ![]()
であることをいう。
関数![]() が
が![]() で微分可能であるならば, 関数
で微分可能であるならば, 関数![]() は
は![]() で連続である。この逆は必ずしも成り立たない。つまり, 関数が連続であっても微分可能とは言えないとうことである。
で連続である。この逆は必ずしも成り立たない。つまり, 関数が連続であっても微分可能とは言えないとうことである。
これは, 関数![]() が
が![]() における微分係数を有限値で持つことである。微分係数とは
における微分係数を有限値で持つことである。微分係数とは![]() における接線の傾きであるため, 連続する関数でも
における接線の傾きであるため, 連続する関数でも![]() における接線の傾きが1つに定まらないものは,
における接線の傾きが1つに定まらないものは, ![]() で微分可能ではないことになる。
で微分可能ではないことになる。
したがって, 微分可能な条件として, ![]()
が有限値で存在し, ![]()
となれば, 微分可能である。
グラフ的に言えば滑らかにつながっていることになる。
以下微分不可能な例を挙げました。
【Case1】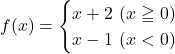

この場合, グラフは
【証明】
このように右側極限と左側極限が一致しない。したがって, 極限
【Case2】
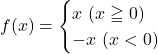
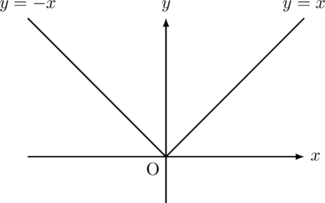
【証明】
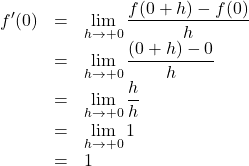
同様に,
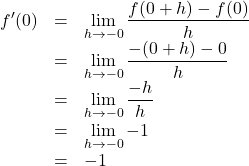
【Case3】
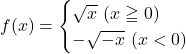
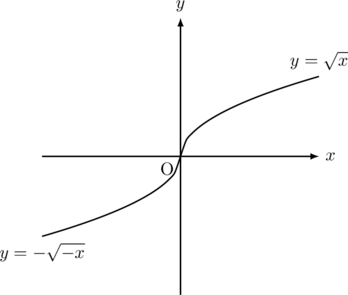
【証明】
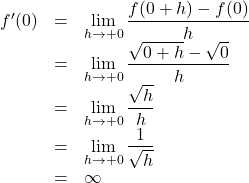
同様に,
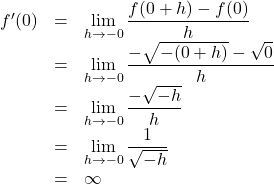
これは
 数樂管理人のブログ
数樂管理人のブログ 

