こんにちは。今回は対数微分法について書いておきます。
対数微分法とは, 関数![]() について, 両辺の絶対値の自然対数をとり, 両辺を
について, 両辺の絶対値の自然対数をとり, 両辺を![]() について微分して導関数を求める方法。
について微分して導関数を求める方法。
以下にその手法を書くと, ![]() として, 両辺の対数をとると,
として, 両辺の対数をとると, ![]()
これを![]() について微分すると,
について微分すると, ![]()
![]()
![]()
よって, ![]()
となり, ![]() の導関数が得られるという手法である。
の導関数が得られるという手法である。
複雑な関数の積や商の微分にも対数微分法は有効である。![]() は,
は, ![]() として, 微分を行うとよい。
として, 微分を行うとよい。
これを![]() について微分すると,
について微分すると, 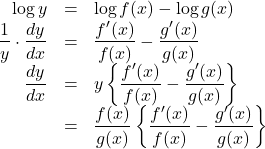
これは, 以下のような関数の微分に有効である。
【例】関数![]() を微分せよ。
を微分せよ。
【解答例】両辺の自然対数をとると, ![]()
この両辺を![]() について微分すると,
について微分すると, 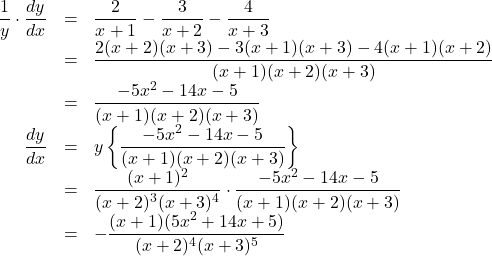
よって, ![]()
【例】関数![]() を微分せよ。
を微分せよ。
【解答例】両辺の自然対数をとると, ![]()
この両辺を![]() について微分すると,
について微分すると, ![Rendered by QuickLaTeX.com \begin{array}{rll}\dfrac{1}{y}\cdot\dfrac{dy}{dx}&=&\dfrac{1}{x}-\dfrac23\cdot\dfrac{2x}{x^2+2}\\&=&\dfrac{3(x^2+2)-4x^2}{3x(x^2+2)}\\\dfrac{dy}{dx}&=&y\left\{\dfrac{6-x^2}{3x(x^2+2)}\right\}\\&=&\dfrac{x}{\sqrt[3]{(x^2+2)^2}}\cdot\dfrac{6-x^2}{3x(x^2+2)}\\&=&\dfrac{6-x^2}{3(x^2+2)\sqrt[3]{(x^2+2)^2}}\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-47f511f652a311a58e1f88aa95dd1ef6_l3.png)
よって, ![]()
![]() を対数微分法で微分してみる。
を対数微分法で微分してみる。![]() として, 両辺
として, 両辺![]() について微分すると,
について微分すると, 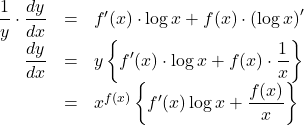
これは, 以下のような関数の微分に有効である。
【例】関数![]() を微分せよ。
を微分せよ。
【解答例】![]() より,
より, ![]()
両辺の自然対数をとって, ![]()
この両辺を![]() について微分し,
について微分し, 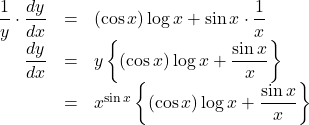
よって, ![]()
【例】関数![]() を微分せよ。
を微分せよ。
【解答例】![]() より,
より, ![]()
両辺の自然対数をとって, ![]()
この両辺を![]() について微分し,
について微分し, 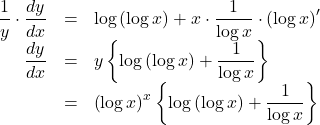
よって, ![]()
最初に示したようにできると思うが, やってみる。
【例】関数![]() を微分せよ。
を微分せよ。
両辺の自然対数をとって, ![]()
この両辺を![]() について微分すると,
について微分すると, 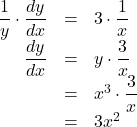
よって, ![]()
どうやら出来そうである。
ただ, 和の形の式には対数はとれないので, 注意は必要である。
 数樂管理人のブログ
数樂管理人のブログ 

