こんにちは。今回は台形の面積の二等分について書いておきます。
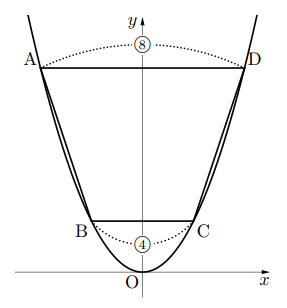
【問】右の図のように, 関数![]() のグラフ上に点A
のグラフ上に点A![]() , B
, B![]() , C
, C![]() , D
, D![]() を頂点とする四角形を作るとき, 頂点Bを通って四角形ABCDの面積を2等分する式を求めなさい。
を頂点とする四角形を作るとき, 頂点Bを通って四角形ABCDの面積を2等分する式を求めなさい。
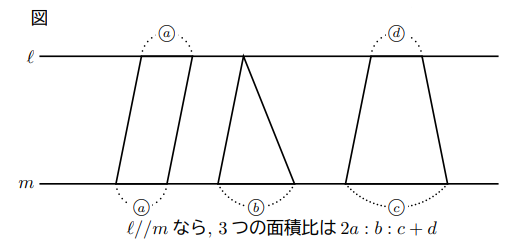
この手の問題の処理方法は, 四角形ABCDは台形であることが多く(別に平行四辺形でもOK), 面積の2等分は(上底![]() 下底)を2等分すればよい。高さの等しい図形の面積比は(上底
下底)を2等分すればよい。高さの等しい図形の面積比は(上底![]() 下底)で表わされるからである(以下図参照)。
下底)で表わされるからである(以下図参照)。
したがって, 上の問題では上底![]() 下底
下底![]() となり, この
となり, この![]() を2等分すれば, 面積は2等分されることになる。このとき求める直線は頂点Bを通ることから, 直線で分けられる図形は三角形と四角形(台形)になる。したがって, この三角形の底辺と台形の上底と下底の和をともに
を2等分すれば, 面積は2等分されることになる。このとき求める直線は頂点Bを通ることから, 直線で分けられる図形は三角形と四角形(台形)になる。したがって, この三角形の底辺と台形の上底と下底の和をともに![]() にするとよい。下底が
にするとよい。下底が![]() なので, 上底は
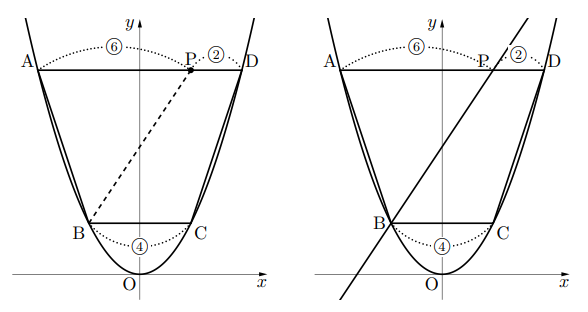
なので, 上底は![]() となる。つまり求める直線は, 点Bと点Dを左に2移動させた点P(2, 8)の2点を通る直線の式である。したがって, 求める直線の式は
となる。つまり求める直線は, 点Bと点Dを左に2移動させた点P(2, 8)の2点を通る直線の式である。したがって, 求める直線の式は![]() である。
である。
 数樂管理人のブログ
数樂管理人のブログ