emath：中学数学：攻略・関数と図形(平行四辺形の面積の2等分)

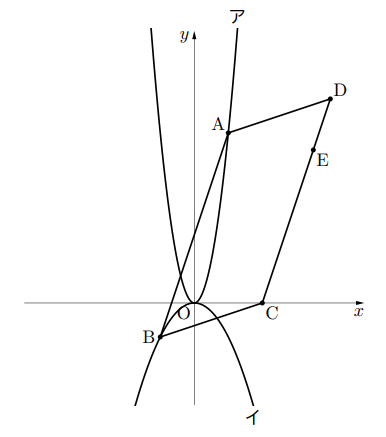
こんにちは。今回は平行四辺形の面積の2等分線の問題を攻略してみようと思います。先ず問題から見ていきましょう。

例題

右の図において, 曲線アは関数 $y=ax^2$ のグラフであり, 曲線イは関数 $y=-\dfrac12x^2$ のグラフである。
曲線ア上の点で $x$ 座標が2である点をA, 曲線イ上の点で $x$ 座標が $-2$ である点をBとする。また, 点Cの座標を $\mathrm{(4, 0)}$ , 点Dの座標を(8, 12)とし, 四角形ABCDは平行四辺形であるものとする。さらに, 辺CD上に点E(7, 9)をとる。
このとき, 次の(1), (2)の問いに答えなさい。ただし, $a>0$ で, Oは原点とする。
(1) $a$ の値を求めなさい。
(2) 点Eを通る直線で, 平行四辺形ABCDを面積の等しい2つの図形に分けるとき, この直線の式を求めなさい。
【茨城】

求めるのは対角線の中点を通る直線

(1)は傾き具合が同じで解ける。Bの座標が $\mathrm{(-2, -2)}$ であり, $\mathrm{C(4, 0)}$ であることから点Bから点Cへは右に6進んで上に2進むとよい。この傾き具合が線分ADでも言えるので, 点Aから点Dへは右に6進んで, 上に2進むと点D $\mathrm{(8, 12)}$ であるから, 逆をたどれば, 点Aは点Dから左に6進んで下に2進んだ点と解釈できる。よって点 $\mathrm{A(8-6, 12-2)}$ からA(2, 10)。これより $y=ax^2$ に代入して, $a=\dfrac52$ を得る。

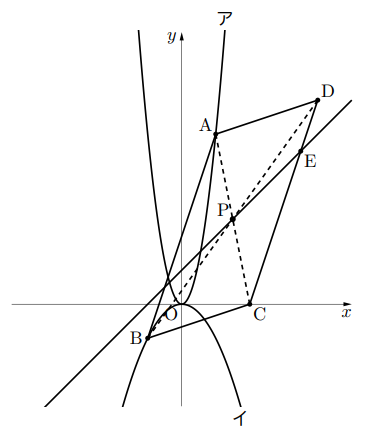
(2)は頻出問題である。平行四辺形の仲間(ひし形,正方形,長方形)の面積の2等分線は必ず対角線の中点を通る。
ここで, 平行四辺形の性質である,「対角線はそれぞれの中点で交わる」ことから2組の向かい合う座標の1組を選んで, 中点を求めればよい。ここでは, A(2, 10)とC(4, 0)の1組を選び中点Pを求めると, $\mathrm{P\left(\dfrac{2+4}{2},\dfrac{10+0}{2}\right)=P(3,5)}$ である。したがって, 求める直線の式は $\mathrm{E(7, 9)}$ と $\mathrm{P(3, 5)}$ を通る直線になる。
それを求めると, $y=x+2$ である。