こんにちは。今回は極限値が与えられた問題での係数決定問題の攻略法を見ていきましょう。
極限の係数決定問題では次の性質をよく利用する。
解法のコツ
![]()
とすると,![]()
![]() として, 係数関係の式をつくる。
として, 係数関係の式をつくる。![]() 分子は
分子は![]() と因数分解できるので,
と因数分解できるので, ![]() として問題解決を図る。
として問題解決を図る。
次の等式が成り立つように, 定数![]() の値を求めよ。
の値を求めよ。
(1) ![]()
(2) ![]()
【解答例】
(1) ![]() のとき, (分母)
のとき, (分母)![]() である。このとき, 分母は,
である。このとき, 分母は, ![]() になる。分母が
になる。分母が![]() に近づくので, 極限値が有限値であるためには,
に近づくので, 極限値が有限値であるためには, ![]() でなくてはならない。
でなくてはならない。
このとき, ![]() とおけるので, これを用いて解法していく。
とおけるので, これを用いて解法していく。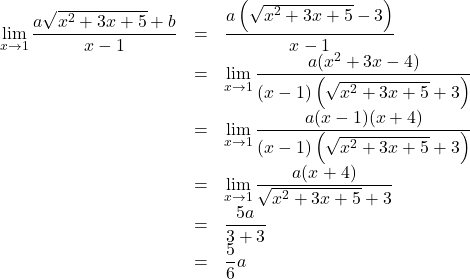
![]() なので,
なので, ![]()
![]()
よって, ![]()
(2) ![]() のとき,
のとき, ![]() であれば, この極限は
であれば, この極限は![]() に発散するので, 有限値を持たない。したがって,
に発散するので, 有限値を持たない。したがって, ![]() である。ここで,
である。ここで, 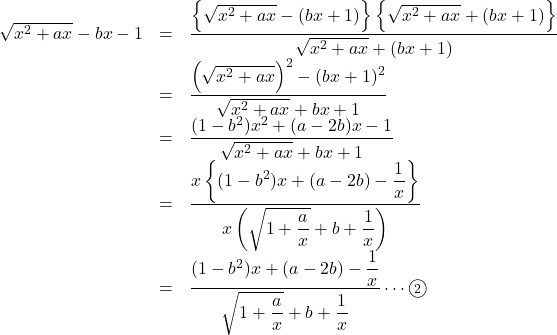
であるから, ![]() が
が![]() のとき, 収束するためには,
のとき, 収束するためには, ![]() の係数が
の係数が![]() である必要がある。
である必要がある。
したがって, ![]() , これと
, これと![]() より,
より, ![]()
![]() として,
として, ![]() の極限を調べると,
の極限を調べると, 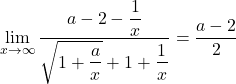
![]()
![]()
よって, ![]()
 数樂管理人のブログ
数樂管理人のブログ 

