こんにちは。今回は三角関数の極限について書いておきます。
三角関数の極限の重要公式
![]()
![]()
![]()
![]()
![]()
![]()
![]() の性質は証明なしで用いてよい。ちなみに証明はこちら
の性質は証明なしで用いてよい。ちなみに証明はこちら
また, 次のような性質がある。![]() ,
, ![]()
ただし, ![]() は
は![]() のとき,
のとき, ![]() になる関数が入る。
になる関数が入る。![]() の証明
の証明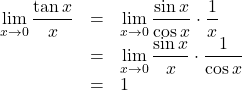
(証明終)
また, 次のような性質がある。![]() ,
, ![]()
ただし, ![]() は
は![]() のとき,
のとき, ![]() になる関数が入る。
になる関数が入る。![]() の証明
の証明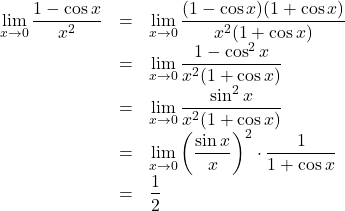
(証明終)
【例】次の極限値を求めよ。
(1) ![]()
(2) ![]()
(3) ![]()
【解答例】
(1) ![]()
(2) ![]() なので,
なので, ![]() とおく, このとき,
とおく, このとき, ![]() で,
で, ![]()
よって, ![]()
(3)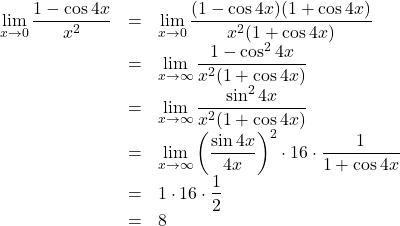
 数樂管理人のブログ
数樂管理人のブログ 

