こんにちは。今回は対数関数の極限について書いておきます。
対数関数![]() は
は![]() かつ
かつ![]() を満たす関数で, 定義域は実数
を満たす関数で, 定義域は実数![]() である。
である。
対数関数のグラフを描くと次のようになる。![]() のとき,
のとき,
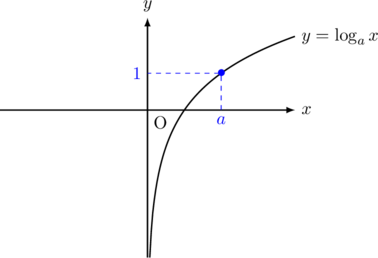
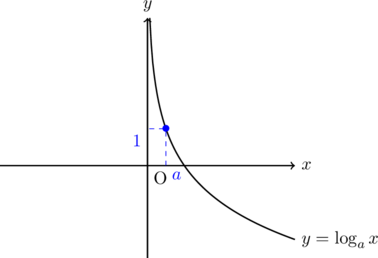
上のグラフからもわかるように, ![]() のとる範囲で指数関数の極限が変わってくる。
のとる範囲で指数関数の極限が変わってくる。
対数関数の極限
![]()
![]() のとき,
のとき,![]() ,
, ![]()
![]()
![]() のとき,
のとき,![]() ,
, ![]()
【例】次の極限を調べよ。
(1) ![]()
(2) ![]()
【解答例】
(1) ![]() のとき
のとき![]() が分かりにくいので,
が分かりにくいので, ![]() とおいて, 考えてみる。
とおいて, 考えてみる。![]() とおくと,
とおくと, ![]()
となるので, ![]()
(2) この場合, 2項をまとめて, ![]() の中の極限を考えるとよい。
の中の極限を考えるとよい。
したがって, 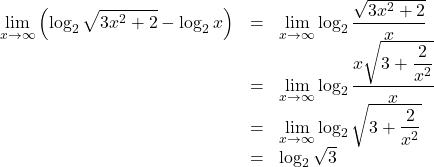
解法のコツ
![]()
![]() の中身が考えにくいときは,
の中身が考えにくいときは, ![]() (
(![]() の中身)とおいて, 極限をとると考えやすい。
の中身)とおいて, 極限をとると考えやすい。![]()
![]() の項が分かれているときは,
の項が分かれているときは, ![]() の性質
の性質![]() や
や![]() を用いて1つにまとめて,
を用いて1つにまとめて, ![]() の中身の極限を考えるとよい。
の中身の極限を考えるとよい。
 数樂管理人のブログ
数樂管理人のブログ 

