こんにちは。今回は平均値の定理について書いておきます。
平均値の定理
関数![]() が閉区間
が閉区間![]() で連続, 開区間
で連続, 開区間![]() で微分可能ならば,
で微分可能ならば, ![]()
を満たす![]() が少なくとも1つは存在する。
が少なくとも1つは存在する。

これの意味するところは, この区間ABにおいて, 直線ABに平行な接線が, 少なくとも1本は引けるということである。したがって, (直線ABの傾き)
また, よくある質問で, 閉区間で連続で, 開区間で微分可能という表現で, 閉区間で微分可能ではだめなのですか?とよく聞かれる。これは関数が閉区間
【例】平均値の定理を用いて, 極限![]() を求めよ。
を求めよ。
【解答例】![]() なので,
なので, ![]() と考えてよい。このとき,
と考えてよい。このとき, ![]() である。
である。
関数![]() はすべての実数
はすべての実数![]() において微分可能である。また,
において微分可能である。また, ![]() より, 閉区間
より, 閉区間![]() において平均値の定理を用いると,
において平均値の定理を用いると, ![]() ,
, ![]()
を満たす![]() が存在する。
が存在する。
ここで, ![]() ,
, ![]() であるから,
であるから, ![]()
よって, ![]()
【例】関数![]() について,
について, ![]() のとき,
のとき, ![]()
を満たす![]() を,
を, ![]() で表せ。また, 極限
で表せ。また, 極限![]() を求めよ。
を求めよ。
【解答例】![]() より,
より, ![]() であるから, これらを与式に代入すると,
であるから, これらを与式に代入すると, ![]()
これを![]() について解く。条件より
について解く。条件より![]() であるから,
であるから, 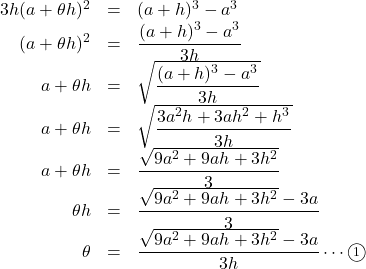
![]() の右辺の分子の有理化を行うと,
の右辺の分子の有理化を行うと, 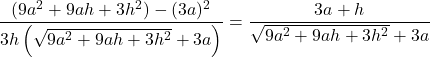
よって, ![]()
以上より, ![]()
![]()
 数樂管理人のブログ
数樂管理人のブログ 

