こんにちは。今回はなぜ積分で面積が求まるのか書いておきます。
関数![]() のグラフが以下のように,
のグラフが以下のように, ![]() となっているとき,
となっているとき, ![]() を定数として, 曲線
を定数として, 曲線![]() ,
, ![]() 軸, 2直線
軸, 2直線![]() で囲まれる図形の面積
で囲まれる図形の面積![]() を考える。
を考える。![]() を変数と考えると,
を変数と考えると, ![]() は
は![]() の関数となる。その関数を
の関数となる。その関数を![]() とおく。
とおく。
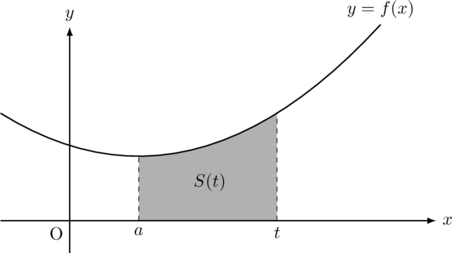
そして,
となる。
よって,
となり, 下線部は微分の定義より,
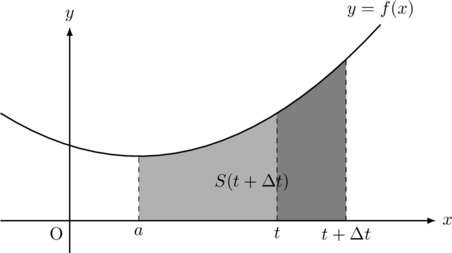
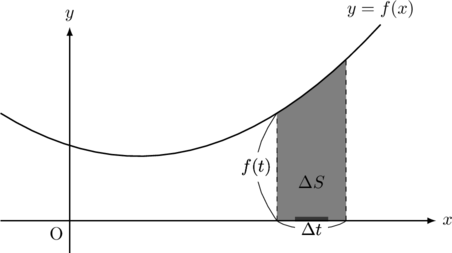
このとき,
となり,
となる。一般に求める面積は
つまりこれは, 曲線
で与えられることが分かる。
こんにちは。今回はなぜ積分で面積が求まるのか書いておきます。
関数![]() のグラフが以下のように,
のグラフが以下のように, ![]() となっているとき,
となっているとき, ![]() を定数として, 曲線
を定数として, 曲線![]() ,
, ![]() 軸, 2直線
軸, 2直線![]() で囲まれる図形の面積
で囲まれる図形の面積![]() を考える。
を考える。![]() を変数と考えると,
を変数と考えると, ![]() は
は![]() の関数となる。その関数を
の関数となる。その関数を![]() とおく。
とおく。


