こんにちは。今回は高次導関数について書いておきます。
関数![]() の導関数
の導関数![]() が微分可能であるとき,
が微分可能であるとき, ![]() を微分して得られる2回微分した関数を
を微分して得られる2回微分した関数を![]() の第2次導関数という。
の第2次導関数という。
一般に, この第2次導関数は, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
などと表す。
以下同様に, ![]() が微分可能なら, これを微分した3回微分の関数を第3次導関数といい,
が微分可能なら, これを微分した3回微分の関数を第3次導関数といい, ![]() ,
, ![]() ,
, ![]() ,
, ![]() などと表す。ただ, 実際のところは3次導関数程度までなら,
などと表す。ただ, 実際のところは3次導関数程度までなら, ![]() ,
, ![]() とすることが多いかもしれない。
とすることが多いかもしれない。
一般に, 関数![]() を
を![]() 回微分して得られる関数を
回微分して得られる関数を![]() の第
の第![]() 次導関数という。
次導関数という。
その表し方は上に習って, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
などと表す。
このように, 第2次導関数以上の導関数をまとめて, 高次導関数という。
【例】関数![]() の第
の第![]() 次導関数を求めよ。
次導関数を求めよ。
【方針】第![]() 次導関数を予測して, 数学的帰納法で証明する。
次導関数を予測して, 数学的帰納法で証明する。
【解答例】![]()
![]()
![]()
これより, 第![]() 次導関数は,
次導関数は, ![]() と予測できる。
と予測できる。
これを数学的帰納法により証明する。![]()
![]() のとき,
のとき, ![]() となり,
となり, ![]() より成り立つ。
より成り立つ。![]()
![]() のとき,
のとき, ![]() が成り立つと仮定すると,
が成り立つと仮定すると, 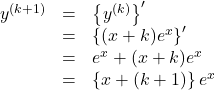
よって, ![]() のときも成り立つ。
のときも成り立つ。
以上から, すべての自然数![]() に対して,
に対して, ![]()
がいえる。
 数樂管理人のブログ
数樂管理人のブログ 

