TikZ：高校数学：数II微分・定数分離の解法を考えてみる

こんにちは。今回は定数分離の解法を見ていこうともいます。あってるかどうかわかりませんが・・・書いておきます。先ずは問題から見ていきましょう。

問題を見てみよう

【例】関数 $f(x)=x^3-4x^2+4x$ と $y=kx$ が $x>0$ の範囲で共有点を2個持つとき, $k$ の範囲を求めよ。

解答例を見てみよう

【解答例】イメージとしては原点を通る直線が, 下図の赤線の直線のように, $x>0$ の範囲で交点を2個持つ感じである。

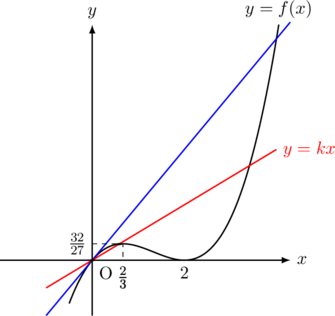
このとき, 赤線の直線は原点を通り, 傾きの $k$ の範囲は, 傾き $k=0$ より大きく, 関数 $f(x)$ に接する直線(青線の直線)の傾き未満までが, この条件を満たすことになる。
原点はこの関数 $f(x)$ のグラフ上の点なので, この点を通る接線の式(青線の式)を求めると, $f'(x)=3x^2-8x+4$ であるから, 接線の傾きは, $f'(0)=4$ 。よって, 接線の式(青線の直線)は $y=4x$
したがって, 求める $k$ の範囲は, $0<k<4$

xで割るとどうなるか

【解答例】さて次はこんなことをやってみようと思う。
関数 $f(x)=x^3-4x^2+4x$ と $y=kx$ が $x>0$ の範囲で共有点を2個持つとあるので,
$x^3-4x^2+4x=kx$ とおいて, $x>0$ なので, $x$ で割って,
$x^2-4x+4=k$
$(x-2)^2=k$ とする。これは, 関数 $y=(x-2)^2$ と直線 $y=k$ のグラフの交点を求めているのに等しく, これが, $x>0$ の範囲で, 交点を2個持てばいいことになる。
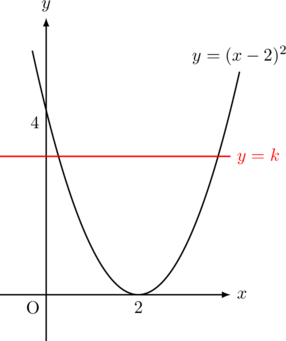
そこでこれを図示すると, 下図のようになり, 黒の曲線 $(y=(x-2)^2)$ と赤の直線 $(y=k)$ が $x>0$ の範囲で交点を2個持つ $k$ の範囲は, $0<k<4$
よって求める $k$ の範囲も $0<k<4$

でも, そもそも $x$ で割っていいものなのか？という疑念は残る。今回はたまたまなのか？誰か教えてほしい。
【その他の解答例】
この問題の解法は他にも $x^3-4x^2+4x=kx$ とおいて, $kx$ を左辺に移項して, $x$ でくくって, 2次方程式をつくり, それが $x>0$ の範囲で異なる2つの実数解をもつように $k$ の範囲を決めるという方法もある。

問題を見てみよう

解答例を見てみよう

xで割るとどうなるか

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル