こんにちは。今回はベクトル方程式と媒介変数について書いておきます。
ベクトル方程式とは, 点![]() が曲線
が曲線![]() 上にあるための位置ベクトル
上にあるための位置ベクトル![]() の条件を等式で表したもの。
の条件を等式で表したもの。
![]() 点
点![]() を通り,
を通り, ![]() に平行な直線のベクトル方程式は,
に平行な直線のベクトル方程式は, ![]()
![]()
![]() のことを方向ベクトルという。
のことを方向ベクトルという。![]() 2点
2点![]() ,
, ![]() を通る直線のベクトル方程式は,
を通る直線のベクトル方程式は, ![]()
 高校数学:平面ベクトルs+t=1のなぜ
高校数学:平面ベクトルs+t=1のなぜ座標平面において, 点![]() を通り, 方向ベクトルが
を通り, 方向ベクトルが![]() の直線
の直線![]() 上の点
上の点![]() は,
は, 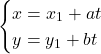
と表すことができる。これを直線![]() の媒介変数表示といい,
の媒介変数表示といい, ![]() を媒介変数という。
を媒介変数という。
【例】点![]() を通り, 方向ベクトル
を通り, 方向ベクトル![]() に平行な直線
に平行な直線![]() を媒介変数
を媒介変数![]() を用いて表し,
を用いて表し, ![]() を消去して, 直線の式を求めよ。
を消去して, 直線の式を求めよ。
【解答例】直線![]() を媒介変数表示すると,
を媒介変数表示すると, 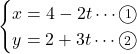
![]() より
より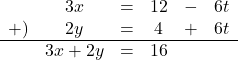
よって, 求める直線の式は![]()
 数樂管理人のブログ
数樂管理人のブログ 

