こんにちは。今回はベクトルの内積について書いておきます。
![]() でない2つのベクトル
でない2つのベクトル![]() について, 始点を
について, 始点を![]() として,
として, ![]() ,
, ![]() とするとき,
とするとき, ![]() を,
を, ![]() と
と![]() のなす角という。ただし,
のなす角という。ただし, ![]() とする。
とする。
このとき, ![]()
を![]() と
と![]() の内積という。
の内積という。![]() または
または![]() が
が![]() の場合,
の場合, ![]() とする。
とする。
また, 内積![]() は実数である。
は実数である。
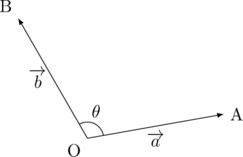
また,
ベクトルのなす角は始点をそろえて考える。
下図で![]() と
と![]() がなす角は
がなす角は![]() ではない。
ではない。![]() は
は![]() が始点であるが,
が始点であるが, ![]() は
は![]() が始点である。したがって, この場合, 始点
が始点である。したがって, この場合, 始点![]() を始点
を始点![]() にそろえるよう,
にそろえるよう, ![]() を平行移動させて,
を平行移動させて, ![]() としてなす角を考える。したがって, この場合,
としてなす角を考える。したがって, この場合, ![]() と
と![]() のなす角は
のなす角は![]() になる。
になる。

【内積の成分表示】![]() ,
, ![]() のとき,
のとき, ![]()
【ベクトルのなす角】![]() ,
, ![]() のとき, この2つのベクトルのなす角
のとき, この2つのベクトルのなす角![]() は,
は, 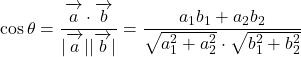
ただし, ![]()
![]() のとき, 2つのベクトルは垂直であるといい, 2つのベクトルが平行のとき,
のとき, 2つのベクトルは垂直であるといい, 2つのベクトルが平行のとき, ![]() であり, 次式が得られる。
であり, 次式が得られる。
【ベクトルの垂直と平行における内積】![]() ,
, ![]()
![]() において,
において, ![]()
![]()
ただし, ![]()
![]() のとき,
のとき, ![]() ,
, ![]() は同じ向きで平行。
は同じ向きで平行。![]()
![]() のとき,
のとき, ![]() ,
, ![]() は反対向きで平行。
は反対向きで平行。
【内積の性質】![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() は実数
は実数![]()
![]() ,
, ![]()
![]() の証明
の証明![]() の各辺に
の各辺に![]() をかけて,
をかけて, ![]()
![]() なので,
なので, ![]()
よって, ![]()
が成り立つ。
内積の性質を用いると, 整式の展開と同じように計算できる。![]()
など
 数樂管理人のブログ
数樂管理人のブログ 

