こんにちは。今回は三角形の重心の位置ベクトルについて書いておきます。
3点![]() ,
, ![]() ,
, ![]() を頂点とする△
を頂点とする△![]() の重心を
の重心を![]() とすると,
とすると, ![]()
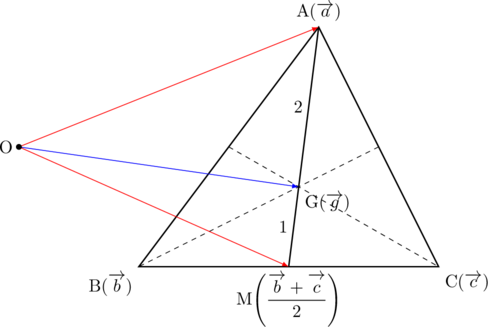
下図のような△![]() において,
において, ![]() は重心で, 位置ベクトルを
は重心で, 位置ベクトルを![]() ,
, ![]() ,
, ![]() ,
, ![]() とすれば,
とすれば, ![]() の中点
の中点![]() の位置ベクトルは
の位置ベクトルは![]() であり, このとき, 重心
であり, このとき, 重心![]() の位置ベクトルは,
の位置ベクトルは, ![]() であるから,
であるから, 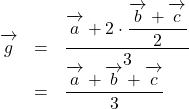
以上より, ![]()
が成り立つ。
また, 点
が成り立つ。
こんにちは。今回は三角形の重心の位置ベクトルについて書いておきます。
3点![]() ,
, ![]() ,
, ![]() を頂点とする△
を頂点とする△![]() の重心を
の重心を![]() とすると,
とすると, ![]()
下図のような△![]() において,
において, ![]() は重心で, 位置ベクトルを
は重心で, 位置ベクトルを![]() ,
, ![]() ,
, ![]() ,
, ![]() とすれば,
とすれば, ![]() の中点
の中点![]() の位置ベクトルは
の位置ベクトルは![]() であり, このとき, 重心
であり, このとき, 重心![]() の位置ベクトルは,
の位置ベクトルは, ![]() であるから,
であるから, 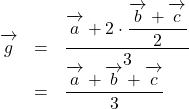
以上より, ![]()
が成り立つ。
