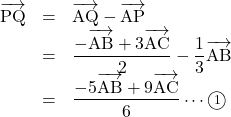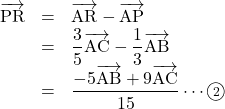こんにちは。今回は3点が一直線上にある条件を書いておきます。
異なる2点![]() ,
, ![]() があるとする。
があるとする。
3点![]() ,
, ![]() ,
, ![]() が一直線上にある。
が一直線上にある。![]() となる実数
となる実数![]() がある。
がある。
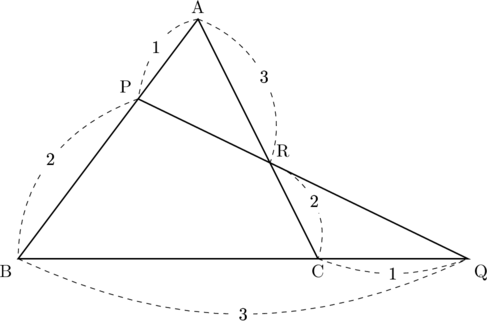
【例】△![]() において, 辺
において, 辺![]() を1 : 2に内分する点を
を1 : 2に内分する点を![]() , 辺
, 辺![]() を3 : 1に外分する点を
を3 : 1に外分する点を![]() , 辺ACを3 : 2に内分する点を
, 辺ACを3 : 2に内分する点を![]() とする。このとき次の問いに答よ。
とする。このとき次の問いに答よ。
(1) ![]() ,
, ![]() ,
, ![]() を
を![]() ,
, ![]() を用いて表せ。
を用いて表せ。
(2) 3点![]() ,
, ![]() ,
, ![]() は一直線上にあることを示せ。
は一直線上にあることを示せ。
【解答例】
(1) 問題文から,
(2) (1)より,
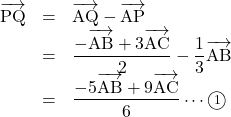
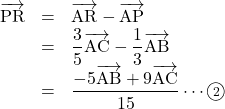
よって, 3点
こんにちは。今回は3点が一直線上にある条件を書いておきます。
異なる2点![]() ,
, ![]() があるとする。
があるとする。
3点![]() ,
, ![]() ,
, ![]() が一直線上にある。
が一直線上にある。![]() となる実数
となる実数![]() がある。
がある。
【例】△![]() において, 辺
において, 辺![]() を1 : 2に内分する点を
を1 : 2に内分する点を![]() , 辺
, 辺![]() を3 : 1に外分する点を
を3 : 1に外分する点を![]() , 辺ACを3 : 2に内分する点を
, 辺ACを3 : 2に内分する点を![]() とする。このとき次の問いに答よ。
とする。このとき次の問いに答よ。
(1) ![]() ,
, ![]() ,
, ![]() を
を![]() ,
, ![]() を用いて表せ。
を用いて表せ。
(2) 3点![]() ,
, ![]() ,
, ![]() は一直線上にあることを示せ。
は一直線上にあることを示せ。
【解答例】