TikZ：高校数学：ベクトル・空間の座標の基本

こんにちは。今回は空間の座標に関して書いておきます。

空間座標

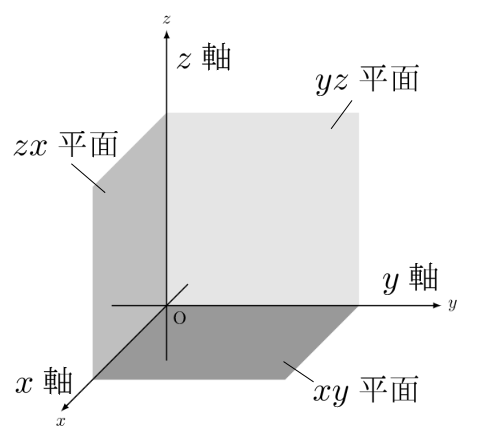
空間において, 原点Oで互いに直交する3本の数直線を定め, それらを $x$ 軸, $y$ 軸, $z$ 軸と呼ぶことにする。この3本をまとめて座標軸という。図のように, 2本の座標軸がつくる平面をそれぞれ $xy$ 平面, $yz$ 平面, $zx$ 平面と呼び, まとめて座標平面という。

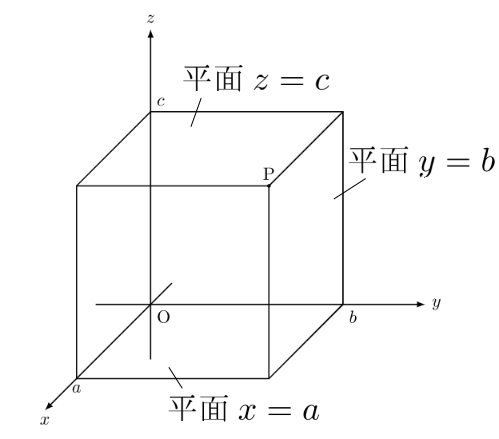
空間内の点Pに対し, 点Pを通り各座標平面に平行な平面が $x$ 軸, $y$ 軸, $z$ 軸と交わる点の座標軸上での座標をそれぞれ, $a$ , $b$ , $c$ とすると, これらは順に点Pの $x$ 座標, $y$ 座標, $z$ 座標となり, まとめて, 点Pの座標を $(a, b, c)$ と表す。

空間内で $x$ 座標が $a$ である点の集合は, 点 $(a, 0, 0)$ を通り, $yz$ 平面に平行な平面である。これを式で表すと, $x=a$ であり, これをこの平面の方程式という。同様に $y$ 座標が $b$ である点の集合を表す平面の方程式は, $zx$ 平面に平行な平面で $y=b$ , $z$ 座標が $c$ である点の集合を表す平面の方程式は, $xy$ 平面に平行な平面で $z=c$ となる。

2点間の距離

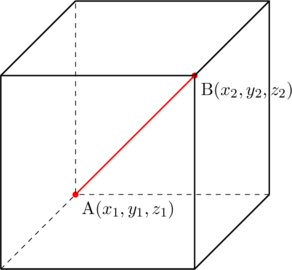
中学生でも履修した三平方の定理を使って, 2点間の距離を求める。
点A $(x_1, y_1, z_1)$ , 点B $(x_2, y_2, z_2)$ とすると,
線分ABの長さは図のような直方体の対角線と捉えることができるので,
$\text{AB}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}$
ちなみに直方体の縦, 横, 高さの3辺はそれぞれ, $|x_2-x_1|$ , $|y_2-y_1|$ , $|z_2-z_1|$ となる。

空間座標

2点間の距離

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル