こんにちは。知っておくと便利な定理を紹介します。使う機会があるかどうかは問題を見てからになるでしょう。紹介するのは, 三角形のおける![]() の定理です。
の定理です。
三角形の3つの内角を![]() とするとき, 成り立つ定理はこちら。
とするとき, 成り立つ定理はこちら。
三角形におけるtanの定理
![]()
三角形の3つの内角を![]() とするとき, 加法定理から,
とするとき, 加法定理から, 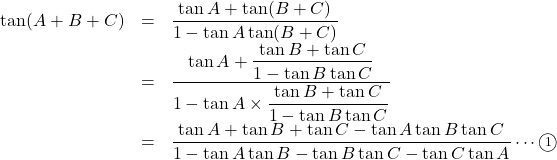
ここで, ![]() なので,
なので, ![]() の左辺の
の左辺の![]() の値は
の値は![]()
よって, ![]() となるので,
となるので, ![]() となり,
となり,
これから, ![]()
を得る。
こんにちは。知っておくと便利な定理を紹介します。使う機会があるかどうかは問題を見てからになるでしょう。紹介するのは, 三角形のおける![]() の定理です。
の定理です。
三角形の3つの内角を![]() とするとき, 成り立つ定理はこちら。
とするとき, 成り立つ定理はこちら。
![]()
三角形の3つの内角を![]() とするとき, 加法定理から,
とするとき, 加法定理から, 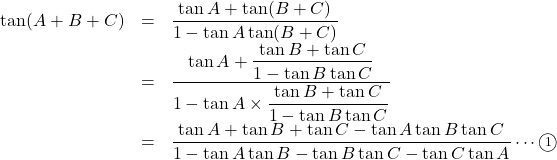
ここで, ![]() なので,
なので, ![]() の左辺の
の左辺の![]() の値は
の値は![]()
よって, ![]() となるので,
となるので, ![]() となり,
となり,
これから, ![]()
を得る。