こんにちは。今回は![]() の微分について書いておきます。証明は
の微分について書いておきます。証明は![]() をそのままでやる場合と,
をそのままでやる場合と, ![]() を
を![]() を用いてやる場合の2通りを書いておきます。それではやっていきましょう。
を用いてやる場合の2通りを書いておきます。それではやっていきましょう。
![]() を導関数の定義にしたがって微分すると,
を導関数の定義にしたがって微分すると, ![]()
となり, 分子の![]() に加法定理を用いると,
に加法定理を用いると, ![]() となり, これを
となり, これを![]() に代入すると,
に代入すると, 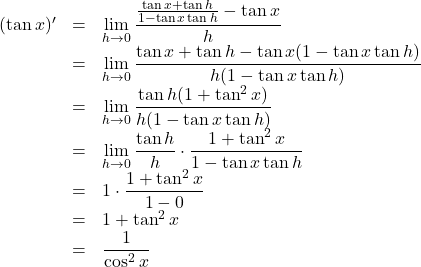
となる。
![]() を導関数の定義にしたがって微分すると,
を導関数の定義にしたがって微分すると, ![]()
![]() の分子を
の分子を![]() を用いて計算してみると,
を用いて計算してみると, 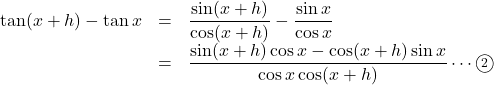
![]() の分子に加法定 理の逆を用いると,
の分子に加法定 理の逆を用いると, ![]()
![]() から,
から, ![]()
![]() を
を![]() に代入すると,
に代入すると, 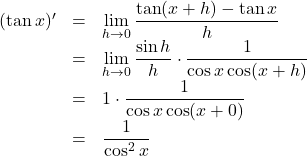
となる。
流れを掴んでおこう
![]() の加法定理を用いて進めるか,
の加法定理を用いて進めるか, ![]() を
を![]() で表して計算して,
で表して計算して, ![]() の加法定理の逆を用いて進めるとよい。
の加法定理の逆を用いて進めるとよい。
 数樂管理人のブログ
数樂管理人のブログ 

