こんにちは。この証明は導出できるように解き方を覚えていた方がいいです。やり方さえ覚えていれば公式はその場で導出できるはずです。それではどうぞ。
![]() を導関数の定義にしたがって微分すると,
を導関数の定義にしたがって微分すると, ![]()
ここで, ![]() を和積の公式で1つにしたいのだが,
を和積の公式で1つにしたいのだが,
和積の公式を忘れたので, それを導出する。![]() の加法定理より,
の加法定理より, ![]()
![]()
![]() を計算すると,
を計算すると, ![]()
左辺と![]() と比較すると,
と比較すると, ![]()
![]()
![]() の連立方程式を解くと,
の連立方程式を解くと, ![]() ,
, ![]()
よって, ![]() より,
より, ![]()
これを用いると, 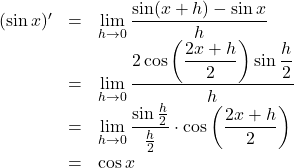
![]() を導関数の定義にしたがって微分すると,
を導関数の定義にしたがって微分すると, ![]()
ここで, ![]() を和積の公式で1つにしたいのだが,
を和積の公式で1つにしたいのだが,
和積の公式を忘れたので, それを導出する。![]() の加法定理より,
の加法定理より, ![]()
![]()
![]() を計算すると,
を計算すると, ![]()
左辺と![]() と比較すると,
と比較すると, ![]()
![]()
![]() の連立方程式を解くと,
の連立方程式を解くと, ![]() ,
, ![]()
よって, ![]() より,
より, ![]()
これを用いると, 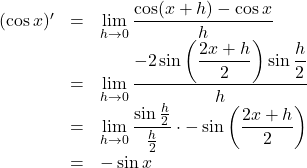
流れを掴んでおこう
![]()
![]() や
や![]() を導関数の定義にしたがって微分する。
を導関数の定義にしたがって微分する。![]()
![]() の分子の差の式を, 和積の公式を用いて, 1つの式にまとめる。
の分子の差の式を, 和積の公式を用いて, 1つの式にまとめる。![]()
![]() の分子の式を
の分子の式を![]() の式で置き換え, 極限をとって終了。
の式で置き換え, 極限をとって終了。
 数樂管理人のブログ
数樂管理人のブログ 
