こんにちは。標準レベルかと思いますが, しっかりと取り組んでいきましょう。
【問題】図のような3辺の長さをもつ三角形ABCがある。
次の問いに答えよ。
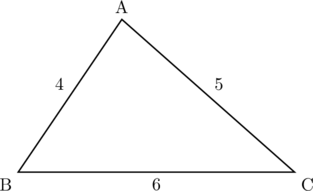
(1)
(2)
(3)
【広島大】
【解答例】
(1) △ABCにおいて余弦定理を用いると, ![]()
![]()
![]()
![]()
ここで, ![]()
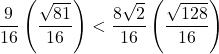
より, ![]() だから,
だから, ![]() とあわせて,
とあわせて, ![]()
(2) △ABCで余弦定理を用いると, ![]()
![]()
![]()
このことから, ![]()
![]() の対辺は最小辺であるから,
の対辺は最小辺であるから, ![]() は大きくても
は大きくても![]() よりは小さい。
よりは小さい。
また, ![]() は
は![]() より小さい正の値であることから,
より小さい正の値であることから, ![]()
がいえる。
(3)
(2)の結果から, ![]()
![]() であり,
であり,
(1)から, ![]() であるから,
であるから, ![]()
![]()
![]()
である。
 数樂管理人のブログ
数樂管理人のブログ 


