受験算数：体積：棒の出し入れの問題(成城中第一回)

こんにちは。入試では定番の問題でしょうか。落としたくないのでやっておきましょう。

2019成城中第一回

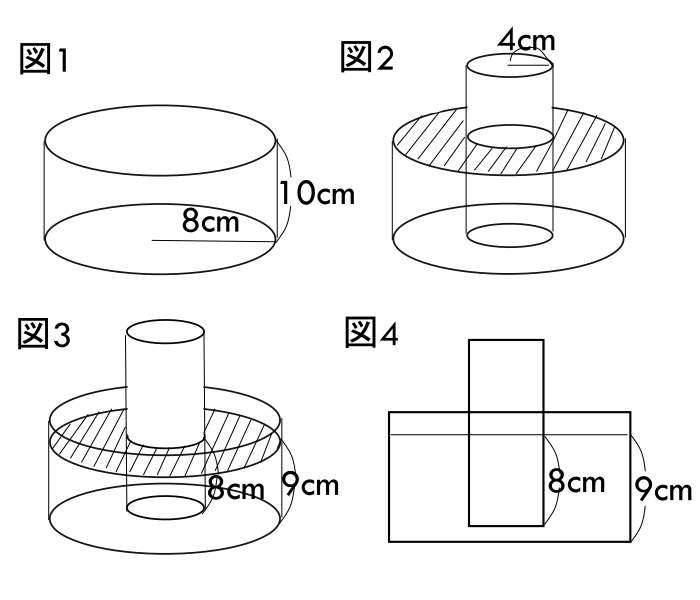
【問題】図1のような円柱の形をした容器に水がいっぱい入っています。
この中に, 底面の半径が4cmの円柱を図2のように底面が容器の底につくまでまっすぐに入れると, 水は【ア】 $\text{cm}^3$ こぼれました。この円柱を取り出した後の水面の高さは【イ】cmでした。
さらに別の円柱をまっすぐに入れていき, 途中で止めたところ, 図3のように, 水面の高さは9cmで, 円柱の水に入っている部分の高さは8cmになりました。図4はこの様子を正面から見た図です。このとき, 入れた円柱の底面積は【ウ】 $\text{cm}^2$ です。

【成城中】

解答例

【解答例】
ア：
初め水面は高さ10cmのところにあったので, こぼれた体積は, 入った棒の体積と同じ。
したがって,
$4\times4\times3.14\times10=502.4$
$502.4\,\text{cm}^3\cdots$ (答)
イ：
初めの水の体積は,
$8\times8\times3.14\times10=2009.6$
なので, 棒を抜いた後の水の体積は,
$2009.6-502.4=1507.2$
$1507.2\div200.96=7.5$
$7.5\text{cm}\cdots$ (答)
ウ：
(初めの水面7.5cmから下に入っている棒の体積) $=$ (水面が増えた体積)
水面が1.5cm上昇して棒の使っている部分が8cmということは, 7.5cm以下の棒の長さは, $8-1.5=6.5(\text{cm})$ となる。
したがって, 求める底面積を $\bigtriangleup$ とすると,
$\bigtriangleup\times6.5=(9-7.5)\times(200.96-\bigtriangleup)$
$\bigtriangleup\times6.5=1.5\times(200.96-\bigtriangleup)$
$6.5\bigtriangleup=301.44-1.5\bigtriangleup$
$\bigtriangleup=301.44\div8=37.68$
$37.68\text{cm}^2\cdots$ (答)

2019成城中第一回

解答例

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル