こんにちは。2次曲線を媒介変数を用いて表すとどうなるか。これについて書いておきます。
媒介変数で表すことの優位性には大きく2つあると思います。
1つ目は式をシンプルに表すことができる。
例えば円の式, ![]() の
の![]() 座標を求める式と言えば, この
座標を求める式と言えば, この![]() 式を
式を![]() について解いて,
について解いて, ![]() みたいになるわけです。そして,
みたいになるわけです。そして, ![]() から,
から, ![]() の範囲を求めて
の範囲を求めて![]() とまぁ面倒なんですよね。
とまぁ面倒なんですよね。
しかし媒介変数を使えば, ![]() 式は,
式は, 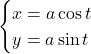
とシンプルに表すことができます。
これが1つ目です。
2つ目は, 媒介変数でしか表せない図形があるからです。例えばサイクロイド曲線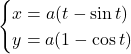
となりますが, ![]() を消去できないので, この表記しかできません。
を消去できないので, この表記しかできません。
このような大きく2つの理由から, 媒介変数表示は用いられていると推察します。
【放物線】![]()
![]()
単純に![]()
![]() , とおくと,
, とおくと, ![]()
よって, 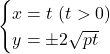
としてもいいのですが, ルートや![]() が出てくるのが厄介だ。ということでもっとシンプルに表せないかということで,
が出てくるのが厄介だ。ということでもっとシンプルに表せないかということで, ![]() との交点を考えて, これを
との交点を考えて, これを![]() 式に代入し,
式に代入し, ![]()
として, 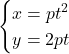
と表すのが一般的である。
【放物線】![]()
![]()
![]() との交点を考えて, これを
との交点を考えて, これを![]() 式に代入し,
式に代入し, ![]()
として, 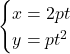
と表される。
【円】![]()
基本思考は![]() の単位円を考える。このとき, 単位円上の点は
の単位円を考える。このとき, 単位円上の点は![]() ,
, ![]() と表される。
と表される。![]() 式は単位円の半径を
式は単位円の半径を![]() 倍したものなので,
倍したものなので, ![]() 座標,
座標, ![]() 座標も
座標も![]() 倍される。
倍される。
よって, 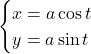
と表される。![]() と
と![]() を入れ換えても成り立つが, 式の意味を考えれば, それは愚問であることがわかる。
を入れ換えても成り立つが, 式の意味を考えれば, それは愚問であることがわかる。
【楕円】![]()
基本思考は![]() の単位円を考える。このとき, 単位円上の点は
の単位円を考える。このとき, 単位円上の点は![]() ,
, ![]() と表される。
と表される。![]() 式は単位円を
式は単位円を![]() 軸方向に
軸方向に![]() 倍,
倍, ![]() 軸方向に
軸方向に![]() 倍したものなので,
倍したものなので, ![]() 座標は
座標は![]() 倍,
倍, ![]() 座標は
座標は![]() 倍される。
倍される。
よって, 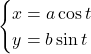
と表される。
【双曲線】![]()
![]() ,
, ![]() とおくと,
とおくと, ![]()
これは2乗したもの同士を引き算して1になる三角関数の公式に着目する。
それがこの公式, ![]()
![]() と
と![]() を比べると,
を比べると, ![]() ,
, ![]() ,
, ![]()
これを![]() について解くと,
について解くと, 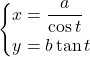
と表される。
【双曲線】![]()
![]() ,
, ![]() とおくと,
とおくと, ![]()
これは2乗したもの同士を引き算して![]() になる三角関数の公式に着目する。
になる三角関数の公式に着目する。
それがこの公式, ![]()
![]() と
と![]() を比べると,
を比べると, ![]() ,
, ![]() ,
, ![]()
これを![]() について解くと,
について解くと, 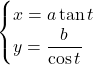
と表される。
 数樂管理人のブログ
数樂管理人のブログ 

