中学数学：攻略法：立体の切断と体積に関する裏技

こんにちは。使い方があってれば非常に便利な公式の紹介。それではいってみましょう。

三角柱の切断体積の裏技

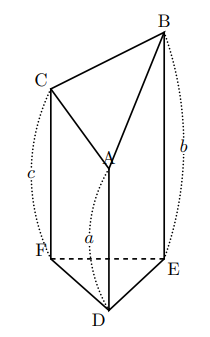
下の立体(三角柱を斜めに切ったもの)の体積 $V$ は底面積を $S$ とすると,
$V=S \times \dfrac{a+b+c}{3}$
で与えられる。

【証明】
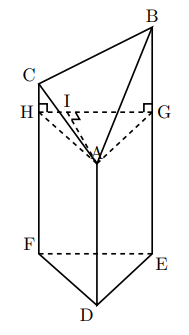
上の立体を下のように底面に平行な面で, 点Aを通る平面AGHで切ると, 底面が台形CHGBの四角錐A $-$ CHGBができる。

その高さをAIとすると, この四角錐の体積は
$\begin{aligned}[t](\text{CH}+\text{BG})\times \text{HG}\times\dfrac12\times \text{AI}&=(\text{CH}+\text{BG})\times \text{HG}\times \text{AI}\times \dfrac12\times\dfrac13\\&=\dfrac13(\text{CH}+\text{BG})\times\bigtriangleup{\text{DEF}}\end{aligned}$
ある。

ここで, 三角柱 $\text{AGH-DEF}$ の体積は次のように書ける。
$\begin{aligned}[t]\bigtriangleup{\text{DEF}}\times \text{AD}&=\bigtriangleup{\text{DEF}}\times (\text{AD}+\text{GE}+\text{HF})\times\dfrac13\end{aligned}$
これより,
もとの立体 $\text{ABC-DEF}$ の体積 $V$ は三角柱 $\text{AGH-DEF+}$ 四角錐 $\text{A-CHGB}$ で求まるので,
$\begin{aligned}[t]V&=\dfrac13(\text{CH}+\text{BG})\times\bigtriangleup{\text{DEF}}+\bigtriangleup{\text{DEF}}\times(\text{AD}+\text{GE}+\text{HF})\times\dfrac13\\&=\bigtriangleup{\text{DEF}}\times\dfrac13{\text{AD}+(\text{BG}+\text{GE})+(\text{CH}+\text{HF})}\\&=S\times\dfrac{a+b+c}{3}\end{aligned}$ \
したがって, 最初の体積の公式が得られる。

直方体の切断体積の裏技

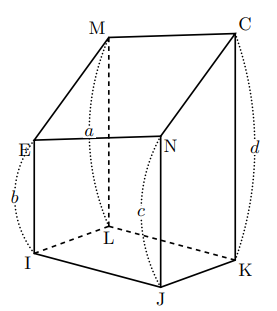
下の立体(直方体を斜めに切ったもの)の体積 $V$ は底面積を $S$ とすると,
$V=S \times \dfrac{a+b+c+d}{4}$
で与えられる。

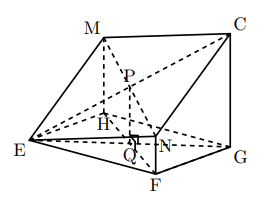
立体の切り口は平行四辺形になる。MC, ENは同一平面上にあり, 面EIJNと面MLKCは平行であるから, MC $//$ EN, 同様にME $//$ CNだから2組の向かい合う辺がそれぞれ平行なので,
四角形MENCは平行四辺形である。

【証明】
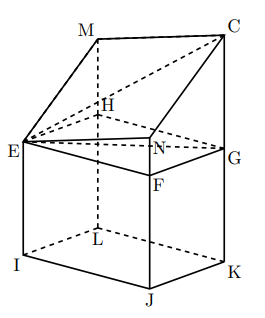
先の立体を立体CNEM $-$ EFGHと直方体EFGH $-$ IJKLに分ける。

そしてさらに立体CNEM $-$ EFGHを2つの切断された三角柱EMC $-$ EGH, ENC $-$ EFGに分ける。

EF $=x$ , FG $=y$ , MH $=e$ ,0(点E) $=f$ , NF $=g$ , CG $=h$ とする。このとき前のページにある切断された三角柱の公式を使うと,
立体 $\text{EMC}-\text{EGH}=xy\times\dfrac12\times\dfrac{e+f+h}{3}$
立体 $\text{ENC}-\text{EFG}=xy\times\dfrac12\times\dfrac{f+g+h}{3}$
この2つを足すと立体CNEM $-$ EFGHが求まるので, 加えると,
$\begin{aligned}[t](\text{CNEM}-\text{EFGH})&=xy\times\dfrac12\times\dfrac{e+f+h}{3}+xy\times\dfrac12\times\dfrac{f+g+h}{3}\\&=xy\times\dfrac{e+g+2f+2h}{6}\cdots\textcircled{\scriptsize{1}}\end{aligned}$
ここで, 平行四辺形MENCの対角線の交点をP, 長方形EFGHの対角線の交点をQとすると, それぞれ対角線の中点で交わるので, 線分PQは長方形EFGHに垂直に交わる。このとき, 中点連結定理を用いると次の関係式が得られる。
$\text{PQ}=\dfrac{e+g}{2}=\dfrac{f+h}{2}$
つまり
$e+g=f+h\cdots\maru2$
である。 $\maru1$ , $\maru2$ より,
$\begin{aligned}[t](\text{CNEM}-\text{EFGH})&=xy\times\dfrac{e+g+2f+2h}{6}\\&=xy\times\dfrac{f+h}{2}\cdots(\alpha)\\&=xy\times\dfrac{2f+2h}{4}\\&=xy\times\dfrac{e+f+g+h}{4}\cdots\textcircled{\scriptsize{3}}\\\end{aligned}$
ただし, 式の途中 $2f+2h=(f+h)+(f+h)=(e+g)+(f+h)$ としている。
また直方体(EFGH $-$ IJKL)の体積は,
$\begin{aligned}[t](\text{EFGH}-\text{IJKL})&=xy\times \text{EI}\\&=xy\times\dfrac{\text{EI}+\text{FJ}+\text{GK}+\text{HL}}{4}\cdots\textcircled{\scriptsize{4}}\end{aligned}$
であるから, $\maru3$ , $\maru4$ より,
もとの立体MENC $-$ IJKLは
$\begin{aligned}[t](\text{MENC}-\text{IJKL})&=(\text{CNEM}-\text{EFGH})+(\text{EFGH}-\text{IJKL})\\&=xy\times\dfrac{e+f+g+h}{4}+xy\times\dfrac{\text{EI}+\text{FJ}+\text{GK}+\text{HL}}{4}\\&=xy\times\dfrac{(e+\text{HL})+(f+\text{HJ})+(g+\text{FJ})+(h+\text{GK})}{4}\\&=xy\times\dfrac{a+b+c+d}{4}\\&=S\times\dfrac{a+b+c+d}{4}\end{aligned}$
となる。

使用例

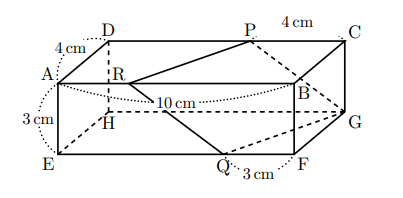
【使用例】図のように, $\text{AB=10 cm}$ , $\text{AD=4 cm}$ , $\text{AE=3 cm}$ の直方体がある。辺CD上に $\text{CP=4 cm}$ となる点P, 辺EF上に $\text{FQ=3 cm}$ となる点Qをとる。さらに, 辺AB上に点Rを4点P, R, Q, Gが同じ平面上にあるようにとると, 四角形PRQGは平行四辺形となる。
このとき, (1)～(3)の各問いに答えなさい。
(1) RQの長さを求めなさい。
(2) RBの長さを求めなさい。
(3) 直方体PRQGで2つの立体に分ける。その2つの立体のうち, 頂点Aを含む立体の体積を $V_1$ , 頂点Bを含む立体の体積を $V_2$ とするとき, $V_1 : V_2$ を最も簡単な整数の比で表わしなさい。

【佐賀県】

この佐賀県の(3)の問題は上の公式を使えば, 体積を求めることなく答えが出せる。
$\text{AR=3 cm}$ , $\text{RB=7 cm}$ であるから, $V_1 : V_2=\dfrac{3+10}{2} : \dfrac{7+0}{2}=13 : 7\cdots$ (答)
ここで, 直方体の場合, 向かい合っている高さを1組選んで平均をとればよい。これは上の $(\alpha)$ の式からも分かる。

注意すべきこと

【余談】前の $\maru1$ 式が得られるための条件は, 四角形を1本の対角線で区切った2つの三角形の面積が等しいことが必要である。
つまり, (底辺) $\times$ (高さ)が等しいことが必要不可欠。ここでは底面が長方形であるから, 面積は等しくなる。底面が台形などでは対角線で区切ると2つの三角形の面積比は, (上底) $:$ (下底)となり, 基本台形では上底と下底は異なるので, この公式は使えないということになる。この公式を理屈を知らずして乱発するのは誤答につながりそうだ。
僕もやってしまいそうである(笑)。でもこの証明は面白かった。では。