こんにちは。数IIの範囲です。早速いってみましょう。
【問題】座標平面上に放物線![]() を考える。次の問いに答えよ。
を考える。次の問いに答えよ。
(1) ![]() と
と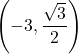 ,
, 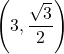 で接している円の方程式を求めよ。
で接している円の方程式を求めよ。
(2) ![]() と(1)の円で囲まれる部分の面積を求めよ。
と(1)の円で囲まれる部分の面積を求めよ。
(3) ![]() と点
と点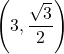 で接し,
で接し, ![]() 軸にも接している円の方程式を求めよ。
軸にも接している円の方程式を求めよ。
(4) ![]() と
と![]() 軸および(3)の円で囲まれる部分の面積を求めよ。
軸および(3)の円で囲まれる部分の面積を求めよ。
【高知大】
 emath:高校数学:積分:放物線と円で囲まれた図形の面積
emath:高校数学:積分:放物線と円で囲まれた図形の面積こんにちは。数IIの範囲です。早速いってみましょう。
【問題】座標平面上に放物線![]() を考える。次の問いに答えよ。
を考える。次の問いに答えよ。
(1) ![]() と
と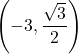 ,
, 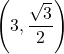 で接している円の方程式を求めよ。
で接している円の方程式を求めよ。
(2) ![]() と(1)の円で囲まれる部分の面積を求めよ。
と(1)の円で囲まれる部分の面積を求めよ。
(3) ![]() と点
と点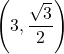 で接し,
で接し, ![]() 軸にも接している円の方程式を求めよ。
軸にも接している円の方程式を求めよ。
(4) ![]() と
と![]() 軸および(3)の円で囲まれる部分の面積を求めよ。
軸および(3)の円で囲まれる部分の面積を求めよ。
【高知大】
 emath:高校数学:積分:放物線と円で囲まれた図形の面積
emath:高校数学:積分:放物線と円で囲まれた図形の面積