こんにちは。ガウス記号と極限です。最後関連記事おいておきます。それではどうぞ。
【問題】実数![]() に対し
に対し![]() を
を![]() を満たす整数とする。次の極限を求めよ。
を満たす整数とする。次の極限を求めよ。
(1) ![Rendered by QuickLaTeX.com \displaystyle\lim_{n\to\infty}\dfrac1n\left[\dfrac{1}{\sin\dfrac1n}\right]](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-c5134048eebb1ffed17d31a8b098e1d2_l3.png)
(2) ![]()
(1) ![]() より,
より, ![Rendered by QuickLaTeX.com \dfrac1n\left(\dfrac{1}{\sin\dfrac1n}-1\right)<\dfrac1n\left[\dfrac{1}{\sin\dfrac1n}\right]\leqq\dfrac1n\cdot\dfrac{1}{\sin\dfrac1n}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-97016e330197a8c092aa79b5e6943f50_l3.png)
が成り立つ。
ここで, 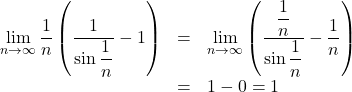
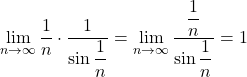
よって, はさみうちの原理より, ![Rendered by QuickLaTeX.com \displaystyle\lim_{n\to\infty}\dfrac1n\left[\dfrac{1}{\sin\dfrac1n}\right]=1](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-13b7865fbc69e2af49e1bb95b99cf585_l3.png)
(2) ![]() より,
より, ![]()
![]()
とすると, ![]() から,
から, ![]()
が成り立つ。![Rendered by QuickLaTeX.com \begin{array}{lll}\displaystyle\lim_{n\to\infty}p_n&=&\displaystyle\lim_{n\to\infty}\displaystyle\dfrac{1}{n\sqrt{n}}\sum_{k=1}^n\left(\sqrt{k}-1\right)\\&=&\displaystyle\lim_{n\to\infty}\left(\dfrac1n\displaystyle\sum_{k=1}^n\sqrt{\dfrac{k}{n}}-\dfrac{n}{n\sqrt{n}}\right)\\&=&\displaystyle\int_0^1\sqrt x\, dx-0\\&=&\left[\dfrac23x^{\frac32}\right]_0^1\\&=&\dfrac23\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-548c1943f25cf3dc2013e7c8df8611b6_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{lll}\displaystyle\lim_{n\to\infty}q_n&=&\displaystyle\lim_{n\to\infty}\displaystyle\dfrac{1}{n\sqrt{n}}\sum_{k=1}^n\sqrt{k}\\&=&\displaystyle\lim_{n\to\infty}\dfrac1n\displaystyle\sum_{k=1}^n\sqrt{\dfrac{k}{n}}\\&=&\displaystyle\int_0^1\sqrt x\, dx\\&=&\left[\dfrac23x^{\frac32}\right]_0^1\\&=&\dfrac23\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-5d78195f7b90aae5b02a92181b4a9f50_l3.png)
よって, はさみうちの原理より,
![]()
 高校数学:数III極限・ガウス記号と極限
高校数学:数III極限・ガウス記号と極限こんにちは。ガウス記号と極限です。最後関連記事おいておきます。それではどうぞ。
【問題】実数![]() に対し
に対し![]() を
を![]() を満たす整数とする。次の極限を求めよ。
を満たす整数とする。次の極限を求めよ。
(1) ![Rendered by QuickLaTeX.com \displaystyle\lim_{n\to\infty}\dfrac1n\left[\dfrac{1}{\sin\dfrac1n}\right]](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-c5134048eebb1ffed17d31a8b098e1d2_l3.png)
(2) ![]()
(1) ![]() より,
より, ![Rendered by QuickLaTeX.com \dfrac1n\left(\dfrac{1}{\sin\dfrac1n}-1\right)<\dfrac1n\left[\dfrac{1}{\sin\dfrac1n}\right]\leqq\dfrac1n\cdot\dfrac{1}{\sin\dfrac1n}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-97016e330197a8c092aa79b5e6943f50_l3.png)
が成り立つ。
ここで, 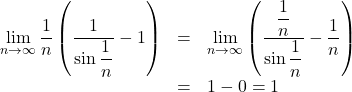
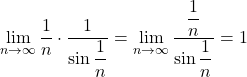
よって, はさみうちの原理より, ![Rendered by QuickLaTeX.com \displaystyle\lim_{n\to\infty}\dfrac1n\left[\dfrac{1}{\sin\dfrac1n}\right]=1](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-13b7865fbc69e2af49e1bb95b99cf585_l3.png)
(2) ![]() より,
より, ![]()
![]()
とすると, ![]() から,
から, ![]()
が成り立つ。![Rendered by QuickLaTeX.com \begin{array}{lll}\displaystyle\lim_{n\to\infty}p_n&=&\displaystyle\lim_{n\to\infty}\displaystyle\dfrac{1}{n\sqrt{n}}\sum_{k=1}^n\left(\sqrt{k}-1\right)\\&=&\displaystyle\lim_{n\to\infty}\left(\dfrac1n\displaystyle\sum_{k=1}^n\sqrt{\dfrac{k}{n}}-\dfrac{n}{n\sqrt{n}}\right)\\&=&\displaystyle\int_0^1\sqrt x\, dx-0\\&=&\left[\dfrac23x^{\frac32}\right]_0^1\\&=&\dfrac23\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-548c1943f25cf3dc2013e7c8df8611b6_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{lll}\displaystyle\lim_{n\to\infty}q_n&=&\displaystyle\lim_{n\to\infty}\displaystyle\dfrac{1}{n\sqrt{n}}\sum_{k=1}^n\sqrt{k}\\&=&\displaystyle\lim_{n\to\infty}\dfrac1n\displaystyle\sum_{k=1}^n\sqrt{\dfrac{k}{n}}\\&=&\displaystyle\int_0^1\sqrt x\, dx\\&=&\left[\dfrac23x^{\frac32}\right]_0^1\\&=&\dfrac23\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-5d78195f7b90aae5b02a92181b4a9f50_l3.png)
よって, はさみうちの原理より,
![]()
 高校数学:数III極限・ガウス記号と極限
高校数学:数III極限・ガウス記号と極限