こんにちは。今回はこういう見方もあるんだというお話です。
2ケタの整数を求める問題で, 以下のような問題を解くときに何か気づくことはあるだろうか?
【問題】2ケタの自然数がある。その数は十の位と一の位の和の6倍に等しく, 十の位と一の位を入れ換えてできる数はもとの数より9小さくなる。もの自然数を求めよ。
である。定石では次のような連立方程式をつくるであろう。
求める自然数の十の位を![]() , 一の位を
, 一の位を![]() とすると,
とすると,
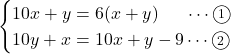
ただ, この問題では![]() の式で十分答えは得られる。
の式で十分答えは得られる。
それはこうだ。![]() 式を計算すると,
式を計算すると, ![]() が得られる。これは
が得られる。これは![]() と同じ意味で, 自然数を表す文字を
と同じ意味で, 自然数を表す文字を![]() として,
として, ![]() とすると,
とすると, ![]() の組み合わせが無数にありそうだが, 問題には2ケタの自然数とあるので, この条件を満たすのは
の組み合わせが無数にありそうだが, 問題には2ケタの自然数とあるので, この条件を満たすのは![]() のときである。したがって, 上の連立方程式の解は,
のときである。したがって, 上の連立方程式の解は, ![]() の式を使わなくとも
の式を使わなくとも![]() である。
である。
よって, 求める自然数は54である。ただし, この方法で全部が全部求められるわけではないことは断っておく。こんなことでも答えは見つかるという例えである。面白いでしょ?
 数樂管理人のブログ
数樂管理人のブログ 

