こんにちは。今回は数学的帰納法です。それではいってみましょう。
【問題】![]() を自然数とするとき,
を自然数とするとき, ![]() は21の倍数であることを, 数学的帰納法によって証明せよ。
は21の倍数であることを, 数学的帰納法によって証明せよ。
【解答】![]() のとき,
のとき,![]() で成り立つ。
で成り立つ。![]() で,
で, ![]() (
(![]() は自然数)
は自然数)![]() が成り立つとすると,
が成り立つとすると, ![]() において,
において,![]()
![]() より,
より, ![]() なので, これを
なので, これを![]() に代入すると,
に代入すると, 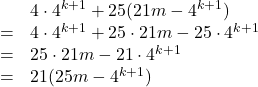
となり, これは21の倍数である。したがって, ![]() においても成り立つ事が言える。
においても成り立つ事が言える。
よって, すべての自然数![]() について成り立つ事が言える。
について成り立つ事が言える。
こんにちは。今回は数学的帰納法です。それではいってみましょう。
【問題】![]() を自然数とするとき,
を自然数とするとき, ![]() は21の倍数であることを, 数学的帰納法によって証明せよ。
は21の倍数であることを, 数学的帰納法によって証明せよ。
【解答】![]() のとき,
のとき,![]() で成り立つ。
で成り立つ。![]() で,
で, ![]() (
(![]() は自然数)
は自然数)![]() が成り立つとすると,
が成り立つとすると, ![]() において,
において,![]()
![]() より,
より, ![]() なので, これを
なので, これを![]() に代入すると,
に代入すると, 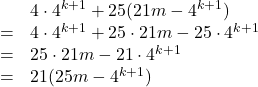
となり, これは21の倍数である。したがって, ![]() においても成り立つ事が言える。
においても成り立つ事が言える。
よって, すべての自然数![]() について成り立つ事が言える。
について成り立つ事が言える。