emath：高校数学：積分：放物線と円で囲まれた図形の面積

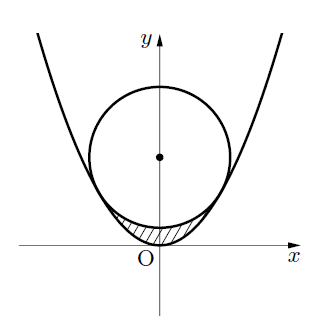
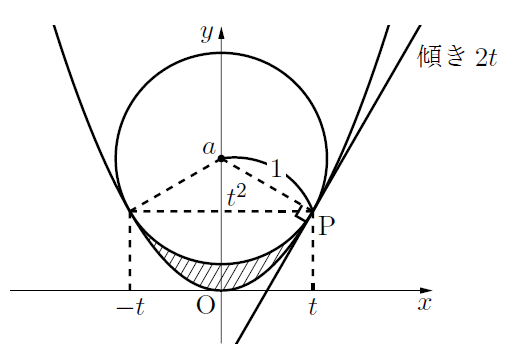
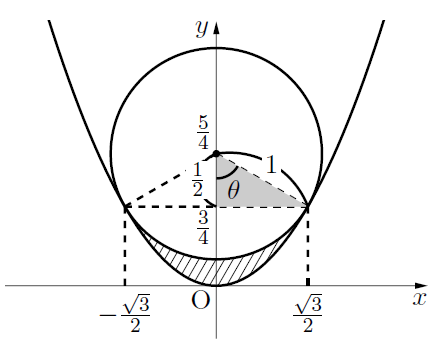
こんにちは。今回は頻出系の問題ということで, 放物線と円で囲まれた図形の面積を求めていきましょう。例題を見ながらいってみましょう。最後に関連記事に演習問題入れています。是非やってみてください。

放物線と円に囲まれた図形の面積

【例題】
(1) $a>1$ のとき, 円 $x^2+(y-a)^2=1$ が放物線 $y=x^2$ と接するような $a$ の値を求めよ。
(2) (1)のとき, 下の図の円と放物線で囲まれた斜線部分の面積を求めよ。

解答例0

【解答例】
(1)

放物線と円の接点の座標の1つをP $( t, t^2)\ t>0$ とおく。このときこの点における放物線の接線の傾きを求めると, $y'=2x$ なので, 点Pにおける接線の傾きは $2t$ となる。
円の半径は接点を通る直線に接点で垂直に交わるので, 円の中心 $(0, a)$ と接点P $(t, t^2)$ を結ぶ傾きは $-\dfrac{1}{2t}$ となる。このことから
$\dfrac{t^2-a}{t-0}=-\dfrac{1}{2t}$
両辺に $t$ をかけて,
$t^2-a=-\dfrac12\cdots\maru1$
また2点 $(0, a)$ とP $(t, t^2)$ の距離は1であるから,
$(t-0)^2+(t^2-a)^2=1\cdots\maru2$
が成り立ち, $\maru1$ を $\maru2$ に代入すると,
$t^2+\left(-\dfrac12\right)^2=1$
$t^2=\dfrac34$
$t>0$ より,
$t=\dfrac{\sqrt3}{2}$
このとき,
$\left(\dfrac{\sqrt3}{2}\right)^2-a=-\dfrac12$
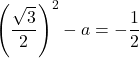
$a=\dfrac54\cdots$ (答)
(2)

接点の座標の1つが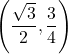 $\left(\dfrac{\sqrt3}{2}, \dfrac34\right)$ であることから, 色のついた三角形は, $1 : 2 : \sqrt3$ の直角三角形になるので, $\theta=\dfrac{\pi}{3}$ となる。
求める面積は直線 $y=\dfrac34$ から放物線 $y=x^2$ を引いたものを $0$ から $\dfrac{\sqrt3}{2}$ で積分し, そこから半径1, 中心角 $\dfrac{\pi}{3}$ の扇形から色のついた直角三角形を引いたものを引いて2倍すればいい。
まとめると次のような式になる。
求める面積を $S$ とすると,
$\begin{array}{lll}S&=&2\left\{\displaystyle\int^{\frac{\sqrt3}{2}}_{0}\left(\dfrac34-x^2\right)\,dx-\left(\dfrac12\cdot1^2\cdot\dfrac{\pi}{3}-\dfrac12\cdot\dfrac{\sqrt3}{2}\cdot\dfrac12\right)\right\}\\&=& 2\left\{\displaystyle\int^{\frac{\sqrt3}{2}}_{0}\left(\dfrac34-x^2\right)\,dx-\left(\dfrac{\pi}{6}-\dfrac{\sqrt3}{8}\right)\right\}\\&=&2 \displaystyle\int^{\frac{\sqrt3}{2}}_{0}\left(\dfrac34-x^2\right)\,dx-2\left(\dfrac{\pi}{6}-\dfrac{\sqrt3}{8}\right) \\ &=&2\left[\dfrac34x-\dfrac13x^3\right]^{\frac{\sqrt3}{2}}_{0}-\dfrac{\pi}{3}+\dfrac{\sqrt3}{4}\\&=&2\cdot\dfrac{\sqrt3}{4} -\dfrac{\pi}{3}+\dfrac{\sqrt3}{4}\\&=&\dfrac{3\sqrt3}{4}-\dfrac{\pi}{3}\end{array}$
よって求める面積は,
$\dfrac{3\sqrt3}{4}-\dfrac{\pi}{3} \cdots$ (答)
※もちろん積分区間をはじめに $-\dfrac{\sqrt3}{2}$ から $\dfrac{\sqrt3}{2}$ として, 扇形の中心角を $\dfrac23\pi$ として計算してもよい。