こんにちは。今回は楕円, 放物線, 双曲線の接線について書いておきます。
楕円の接線
楕円の接線
楕円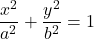 上の点
上の点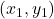 における接線の方程式は
における接線の方程式は
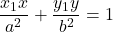
で与えられる。
で与えられる。
【証明】![]() の両辺を
の両辺を![]() で微分すると,
で微分すると, ![]()
![]()
![]()
となるので, 接線の方程式は傾きが![]() で, 点
で, 点![]() を通る直線になる。
を通る直線になる。
したがって, 次のような式になる。 ![]()
両辺![]() かけて, 展開すると,
かけて, 展開すると, ![]()
![]()
両辺![]() で割ると,
で割ると, ![]()
![]() の右辺において,
の右辺において, ![]() は楕円上の点であるから,
は楕円上の点であるから, ![]() が成り立つので,
が成り立つので, ![]() から
から
接線の方程式![]()
を得る。
双曲線の接線
双曲線の接線
双曲線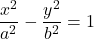 上の点
上の点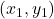 における接線の方程式は
における接線の方程式は
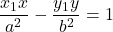
で与えられる。
で与えられる。
【証明】
双曲線![]() 上の点
上の点![]() における接線の方程式は
における接線の方程式は![]()
で与えられる。
【証明】![]() の両辺を
の両辺を![]() で微分すると,
で微分すると, ![]()
![]()
![]()
となるので, 接線の方程式は傾きが![]() で, 点
で, 点![]() を通る直線になる。
を通る直線になる。
したがって, 次のような式になる。 ![]()
両辺![]() かけて, 展開すると,
かけて, 展開すると, ![]()
![]()
両辺![]() で割ると,
で割ると, ![]()
![]() の右辺において,
の右辺において, ![]() は楕円上の点であるから,
は楕円上の点であるから, ![]() が成り立つので,
が成り立つので, ![]() から
から
接線の方程式![]()
を得る。
放物線y²=4pxの接線
放物線の接線
放物線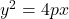 上の点
上の点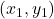 における接線の方程式は
における接線の方程式は
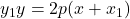
で与えられる。
で与えられる。
【証明】![]() の両辺を
の両辺を![]() で微分すると,
で微分すると, ![]()
![]()
となるので, 接線の方程式は傾きが![]() で, 点
で, 点![]() を通る直線の式になる。
を通る直線の式になる。
したがって, 次のような式になる。![]()
両辺に![]() をかけて, 展開すると,
をかけて, 展開すると, ![]()
ここで, ![]() は放物線上の点であるから,
は放物線上の点であるから, ![]() が成り立つ。これを
が成り立つ。これを![]() の
の![]() と置き換えると,
と置き換えると, ![]()
![]() となり,
となり,
接線の方程式![]()
を得る。
 数樂管理人のブログ
数樂管理人のブログ 

