こんにちは。公立高校の一般選抜試験から大問2を解説していきます。
【問題】かずきさんとみさきさんは, 厚紙を切って, 3種類の図形A, B, Cをたくさんつくっている。図形Aは正方形, 図形Bは1辺の長さが図形Aの1辺の長さと等しく, 他方の辺の長さが1cmの長方形, 図形Cは1辺の長さが1cmの正方形である。(1)・(2)に答えなさい。
(1) 厚紙は, 赤, 青, 白, 黄, 緑の5色ある。この5色から3色選ぶとき, その選び方は全部で何通りあるか, 求めなさい。
(2) 2人は, 図形A, B, Cを何枚か組み合わせて, 重ならないようにすき間なくしきつめ, いろいろな四角形をつくろうと考えている。図形Aの1辺の長さを![]() cmとして, (a)~(c)に答えなさい。
cmとして, (a)~(c)に答えなさい。
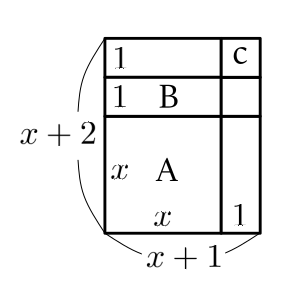
(a) 図形Aを1枚, 図形Bを3枚, 図形Cを2枚の合計6枚を組み合わせると, 1つの長方形をつくることができる。![]() のとき, この長方形の2辺の長さは, それぞれ何cmか, 求めなさい。
のとき, この長方形の2辺の長さは, それぞれ何cmか, 求めなさい。
(b) かずきさんは, 図形Aを1枚, 図形Bを6枚, 図形Cを8枚の合計15枚を組み合わせて, 1枚の長方形をつくった。この長方形の周の長さを![]() を用いて表しなさい。
を用いて表しなさい。
(c) みさきさんは, 図形A, B, Cを何枚か組み合わせて, 1辺の長さが![]() cmの正方形を1つつくった。この正方形の面積は, 図形Aを1枚, 図形Bを6枚, 図形Cを8枚の合計15枚を組み合わせてかずきさんがつくった1つの長方形の面積より105cm
cmの正方形を1つつくった。この正方形の面積は, 図形Aを1枚, 図形Bを6枚, 図形Cを8枚の合計15枚を組み合わせてかずきさんがつくった1つの長方形の面積より105cm![]() 大きかった。このとき,
大きかった。このとき, ![]() の値を求めなさい。
の値を求めなさい。
「2022年徳島県公立高校入試」
(1) 5つから3つ選ぶとき, 必ず2つ残る。このことに着目すると, 5つから3つ選ぶことは5つから2つ選んで残った3つを選んでいけばいいことになる。つまり, 5つから3つ選ぶ場合の数は, 5つから2つ選ぶ場合の数と等しくなる。よって, 答えは 10通り
(2)
(a)面積に着眼すると, 図形Aは![]() cm
cm![]() , 図形Bは
, 図形Bは![]() cm
cm![]() , 図形Cは1cm
, 図形Cは1cm![]() なので, この図形A, B, Cをそれぞれ, 1枚, 3枚, 2枚合わせた面積は,
なので, この図形A, B, Cをそれぞれ, 1枚, 3枚, 2枚合わせた面積は, ![]() となり, 因数分解すると,
となり, 因数分解すると, ![]() となる。
となる。 ![]() なので, 代入すると,
なので, 代入すると, ![]() となる。したがって, 4cmと5cmとなる。
となる。したがって, 4cmと5cmとなる。
4cm, 5cm![]() (答)
(答)
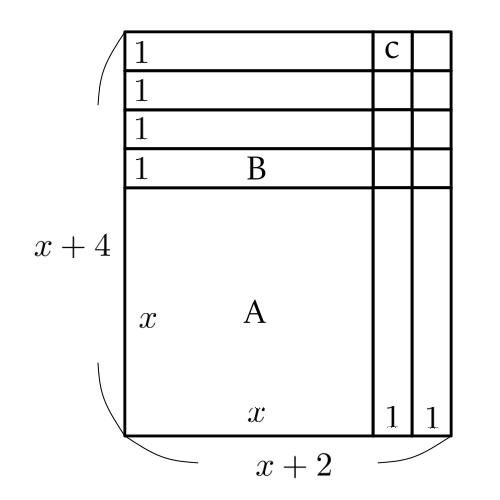
(b) (a)と同様面積に着目すると, 図形Aが1枚, 図形Bが6枚, 図形Cが8枚なので, 面積は![]() (cm
(cm![]() )になり, 因数分解すると,
)になり, 因数分解すると, ![]() になる。したがって, 2つの辺の長さは,
になる。したがって, 2つの辺の長さは, ![]() (cm),
(cm), ![]() (cm)となるので, 求める周の長さは
(cm)となるので, 求める周の長さは![]() (cm)
(cm)![]() (cm)
(cm)![]() (答)
(答)
(c) 問題から方程式をつくると,![]()
![]()
![]()
![]() (答)
(答)
【余談】(2)の(a)はこう並べるのは愚問なのだろうか。完全ボヤキです。
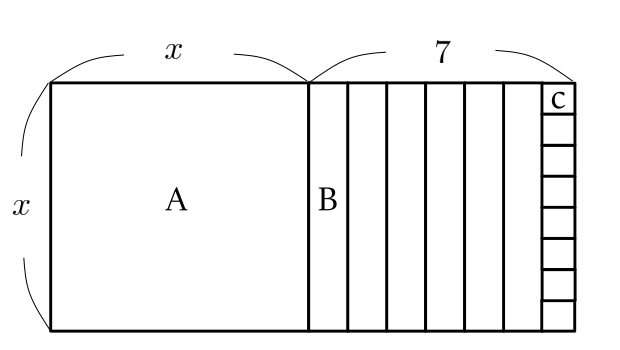
この場合だと, 周の長さは![]() (cm)になるが,
(cm)になるが, ![]() が変数でなくなる(
が変数でなくなる(![]() 固定)からダメなんだろうな。
固定)からダメなんだろうな。
 数樂管理人のブログ
数樂管理人のブログ 


