こんにちは。今回は中間値の定理について書いておきます。
中間値の定理
関数![]() が閉区間
が閉区間![]() で連続で,
で連続で, ![]() ならば,
ならば, ![]() と
と![]() の間の任意の値
の間の任意の値![]() に対して,
に対して,![]() ,
, ![]()
を満たす![]() が少なくとも1つ存在する。
が少なくとも1つ存在する。
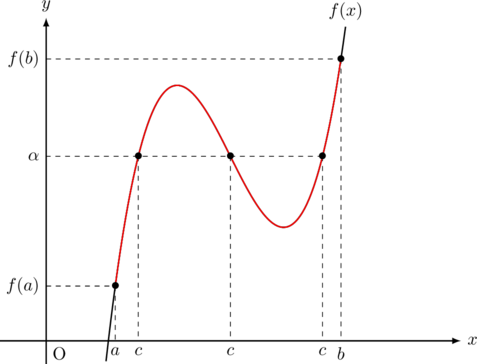
![]() と
と![]() が異符号なら, 次の事が言える。
が異符号なら, 次の事が言える。
実数解の存在
関数![]() が区間
が区間![]() で連続で,
で連続で, ![]() と
と![]() が異符号
が異符号![]() なら,
なら,
方程式![]() は区間
は区間![]() に少なくとも1つの実数解をもつ。
に少なくとも1つの実数解をもつ。
【例】方程式![]() が,
が, ![]() で少なくとも1つの実数解をもつように, 定数
で少なくとも1つの実数解をもつように, 定数![]() の範囲を求めよ。
の範囲を求めよ。
【解答例】![]() とおくと,
とおくと, ![]() は
は![]() で連続であるから,
で連続であるから, ![]() と
と![]() の値が異符号であることが条件になる。
の値が異符号であることが条件になる。
したがって, ![]() が求める条件になる。
が求める条件になる。
ここで, ![]() ,
, ![]() なので,
なので, ![]() より,
より, ![]()
よって, 求める範囲は, ![]()
※もし問題で, ![]() のように不等号に等号が付いていたなら, 区間の端点を含む場合も入れるので,
のように不等号に等号が付いていたなら, 区間の端点を含む場合も入れるので, ![]() とすればよい。
とすればよい。
 数樂管理人のブログ
数樂管理人のブログ 

