こんにちは。基本問題かと思いますので, やっていきましょう。
【問題】座標空間において, 3点A(1, 0, 0), B(0, 2, 0), C(0, 0, 2)を通る平面を![]() とする。3点A, B, Cを通る球面の中心Mが平面
とする。3点A, B, Cを通る球面の中心Mが平面![]() 上にあるとき, Mの座標と球面の半径
上にあるとき, Mの座標と球面の半径![]() を求めよ。
を求めよ。
【信州大】
【解答例】
△ABCは![]() の二等辺三角形なので, 球の中心Mは頂角Aの二等分線上にある。
の二等辺三角形なので, 球の中心Mは頂角Aの二等分線上にある。
また, A, B, Cを通ることから, Mは△ABCの外心である。
頂角Aの二等分線と底辺BCの交点をNとすると, Nの座標はBCの中点であるから, ![]() である。
である。
このとき, ![]() なので,
なので, ![]() 。
。
よって, ![]() である。
である。![]() ,
, ![]() なので,
なので, ![]()
![]() なので,
なので, ![]()
これを解いて, ![]()
![]()
![]() なので,
なので, 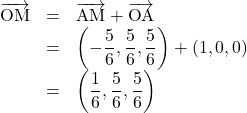
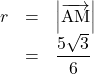
以上より, ![]() ,
, ![]()
 数樂管理人のブログ
数樂管理人のブログ 


