こんにちは。それでは早速いってみましょう。
下の図1は, ![]() cm,
cm, ![]() の直角二等辺三角形ABCを底面とし,
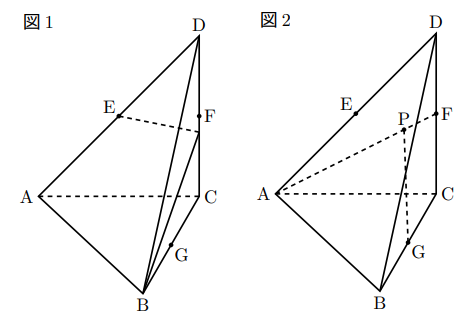
の直角二等辺三角形ABCを底面とし, ![]() cmを高さとする三角すいである。また, 3点E, F, Gはそれぞれ辺AD, 辺CD, 辺BCの中点である。このとき, 次の問いに答えなさい。
cmを高さとする三角すいである。また, 3点E, F, Gはそれぞれ辺AD, 辺CD, 辺BCの中点である。このとき, 次の問いに答えなさい。
(1) この三角すいの体積を求めなさい。
(2) この三角すいの表面上に, 点Bから辺CDと交わるように, 点Eまで線を引く。このような線のうち, 長さが最も短くなるように引いた線の長さを求めなさい。
(3) 下の図2のように, この三角すいの線分AF上に点Pを線分AFと線分GPが垂直となるようにとる。このとき, 線分GPの長さを求めなさい。
【神奈川県】
 数樂管理人のブログ
数樂管理人のブログ