こんにちは。今回は累乗根の大小関係について書いておきます。今回は底がそろう場合ですが, 底が異なる場合はこちらを参照ください。
累乗根の大小関係は, 底をそろえて, 指数部分の大小関係で決着させることが多い。
底![]() が1より大きいとき, すなわち,
が1より大きいとき, すなわち, ![]() の場合,
の場合, ![]()
が成り立つ。このことは, 以下のグラフからもわかる。
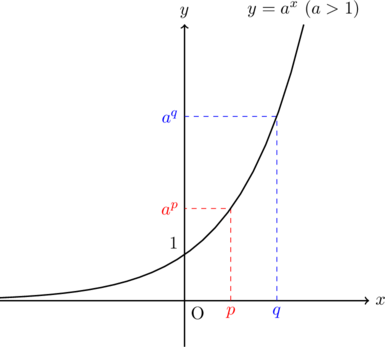
底
が成り立つ。このことは, 以下のグラフからもわかる。
累乗根の大小関係
![]() 底
底![]() が1より大きいとき, すなわち,
が1より大きいとき, すなわち, ![]() の場合,
の場合, ![]() 指数部の大小と元の数の大小関係が一致する。
指数部の大小と元の数の大小関係が一致する。![]() 底
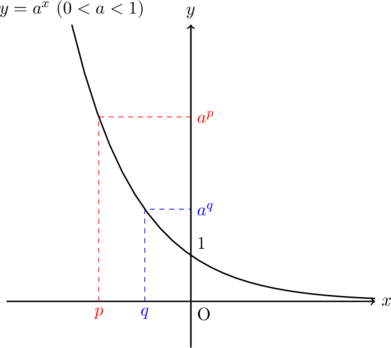
底![]() が0と1の間にあるとき, すなわち,
が0と1の間にあるとき, すなわち, ![]() の場合,
の場合, ![]() 指数部の大小と元の数の大小関係が逆になる。
指数部の大小と元の数の大小関係が逆になる。
以上のことをふまえて例題を見てみましょう。
【例題】![]() の大小関係を調べ, 不等号を用いて表せ。
の大小関係を調べ, 不等号を用いて表せ。
【解法】底を5でそろえると, ![]() ,
, ![]() ,
, ![]()
底5は1より大きいので, 指数部の大小関係と, 元の数の大小関係は一致するので, 指数部を比べると, ![]() なので,
なので, ![]()
よって, ![]()
【例題】![]() の大小関係を調べ, 不等号を用いて表せ。
の大小関係を調べ, 不等号を用いて表せ。
【解法】底が0と1の間の数なので, 指数部の大小関係と逆の関係が元の数の大小関係になるので, 指数部を比べると, ![]() なので, 元の数の大小関係はその逆になる。
なので, 元の数の大小関係はその逆になる。
よって, ![]()
 数樂管理人のブログ
数樂管理人のブログ 

