こんにちは。今回は数IIIの微分の仕方について書いておきます。
導関数の定義![]()
詳しくは以下の記事を
 emath:高校数学:微分と接線の傾き
emath:高校数学:微分と接線の傾き![]() (
(![]() は定数)
は定数)![]()
特に![]() が成り立つ。(
が成り立つ。(![]() は実数)
は実数)
 高校数学:微分:xⁿを微分するとnxⁿ⁻¹になるわけ
高校数学:微分:xⁿを微分するとnxⁿ⁻¹になるわけまた, ![]() は
は![]() として
として![]() の微分を行うと,
の微分を行うと, ![]()
となり, ![]() の微分は
の微分は![]() として
として![]() の微分を行うと,
の微分を行うと, ![]() 。
。
となる。![]() (複合同順)
(複合同順)![]()
特に, ![]()
 高校数学:数III微分:積の微分のなぜ・3つの積の微分は?
高校数学:数III微分:積の微分のなぜ・3つの積の微分は?![]()
特に, ![]()
 高校数学:数III:微分:商の微分の公式のなぜ
高校数学:数III:微分:商の微分の公式のなぜ次の関数を微分せよ。![]()
![]()
![]()
![]()
![]()
![]()
![]()
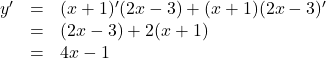
別に展開してから微分しても問題ない。![]() となるので,
となるので, ![]()
よって, ![]()
![]()
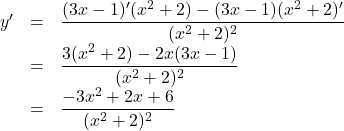
![]()
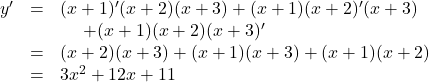
 数樂管理人のブログ
数樂管理人のブログ 

