こんにちは。今回は図形の面積が定積分で与えられることを書いておきます。
【パターン1】
以下の図形の面積![]() は次の定積分で与えられる。
は次の定積分で与えられる。![]()
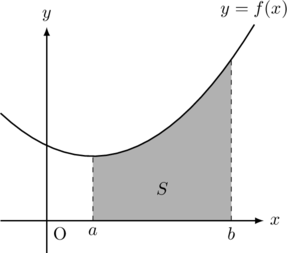
【パターン2】
以下の図形の面積
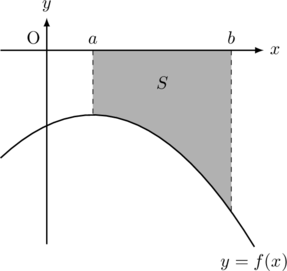
【パターン3】
以下の図形の面積
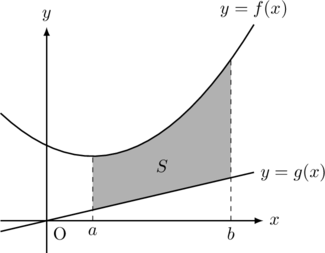
【パターン4】
以下の図形の面積
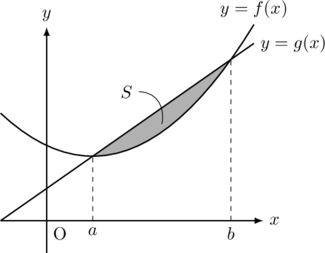
パターン3, 4から分るように, 2つのグラフに囲まれた面積を求める場合は, 上にあるグラフから下にあるグラフを引いて, 積分すればよいことになる。
 TikZ:高校数学:積分・定積分と面積(なぜ積分で面積が求まるのか)
TikZ:高校数学:積分・定積分と面積(なぜ積分で面積が求まるのか)こんにちは。今回は図形の面積が定積分で与えられることを書いておきます。
【パターン1】
以下の図形の面積![]() は次の定積分で与えられる。
は次の定積分で与えられる。![]()




 TikZ:高校数学:積分・定積分と面積(なぜ積分で面積が求まるのか)
TikZ:高校数学:積分・定積分と面積(なぜ積分で面積が求まるのか)