こんにちは。早速やってみましょう。
【問題】![]() ,
, ![]() とし, 媒介変数表示
とし, 媒介変数表示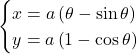
で表される曲線のグラフをかき, その長さを求めよ。
【解答例】![]() を
を![]() で微分すると,
で微分すると, ![]() となる。
となる。![]() の範囲では,
の範囲では, ![]() なので,
なので, ![]() である。
である。
したがって, ![]() が増加すれば,
が増加すれば, ![]() の値も増加する。
の値も増加する。![]() を
を![]() で微分すると,
で微分すると, ![]() となる。
となる。![]() において,
において, ![]() は,
は, ![]() で
で![]() であるから,
であるから, ![]() で,
で, ![]() で
で![]() であるから,
であるから, ![]() である。
である。
したがって, ![]() の値は,
の値は, ![]() で増加し,
で増加し, ![]() で減少する。
で減少する。
これをもとにグラフを描くと以下のようになる。
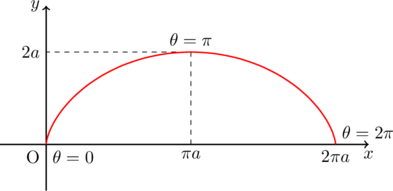
次に曲線の長さを求める。
求める長さを
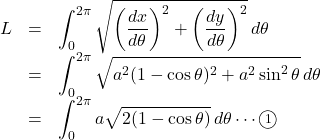
半角の公式より,
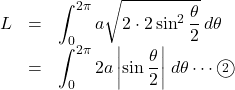
よって,
![Rendered by QuickLaTeX.com \begin{array}{lll}L&=&\displaystyle\int_0^{2\pi}2a\sin\dfrac{\theta}{2}\, d\theta\\&=&2a\left[-2\cos\dfrac{\theta}{2}\right]_0^{2\pi}\\&=&2a\left\{2-(-2)\right\}\\&=&8a\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-dcfb17ff0a4a9867536218ad606bba89_l3.png)
よって曲線の長さは
この曲線はサイクロイド曲線と言います。以下の関連記事に性質をまとめています。ご覧ください。
 TikZ:高校数学:数IIIグラフ:サイクロイド曲線とその性質
TikZ:高校数学:数IIIグラフ:サイクロイド曲線とその性質 数樂管理人のブログ
数樂管理人のブログ 


