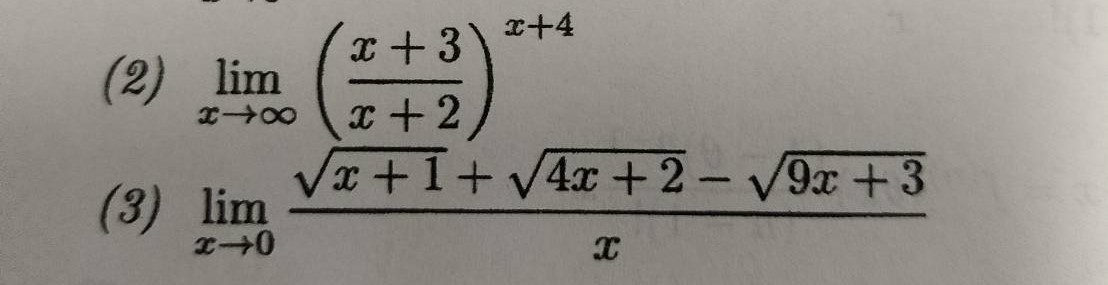図形 数学1A 緊急です！
MFを求めるところから解説おねがいします
平野
Re: 図形 数学1A
管理人 
2023/08/08(Tue) 08:51 No.84
AE:EC=3:2,AD:DM=2:1より
メネラウスの定理を用いる。
MF=xとすると、FC=x+2なので
2/1×MF/FC×2/3=1
2/1×x/(x+2)×2/3=1
4x=3(x+2)
x=6→MF
aとcの2組だと思う自信はないが
理由はともに同位角が90度で等しいから。
△ABCで余弦定理よりcos∠ACB＝1/√10, sin∠ACB=3/√10
△ACFで余弦定理よりAF＝6√2
正弦定理から△ACFの外接円の半径Rを求めると
R＝2√5
よってJC＝4√5
FC＝8より, △JFCで三平方の定理から
JF＝4
以上になります。
今後答えや解説付けてくださいね。
ないなら仕方ないですが
メネラウスの定理を用いる。
MF=xとすると、FC=x+2なので
2/1×MF/FC×2/3=1
2/1×x/(x+2)×2/3=1
4x=3(x+2)
x=6→MF
aとcの2組だと思う自信はないが
理由はともに同位角が90度で等しいから。
△ABCで余弦定理よりcos∠ACB＝1/√10, sin∠ACB=3/√10
△ACFで余弦定理よりAF＝6√2
正弦定理から△ACFの外接円の半径Rを求めると
R＝2√5
よってJC＝4√5
FC＝8より, △JFCで三平方の定理から
JF＝4
以上になります。
今後答えや解説付けてくださいね。
ないなら仕方ないですが
管理人 2023/08/08(Tue) 08:51 No.84
半順序
{1, 3, 5}が≦の関係を満たすとき、これは半順序ですか？
1.反射律: 1 ≤ 1, 2 ≤ 2, 3 ≤ 3, 4 ≤ 4.
2.反対称律: a ≤ b, b ≤ a, → a=b.が成り立つのはa=bしかありえません。よって、反対称律が満たされます
3.推移律: 1 ≤ 2, 2 ≤ 3, 3 ≤ 4 →1 ≤ 4.
よって半順序だと思うのですが、正解ですか？
もし正解ではなかったら、半順序の例を提示してくてると助かります
1.反射律: 1 ≤ 1, 2 ≤ 2, 3 ≤ 3, 4 ≤ 4.
2.反対称律: a ≤ b, b ≤ a, → a=b.が成り立つのはa=bしかありえません。よって、反対称律が満たされます
3.推移律: 1 ≤ 2, 2 ≤ 3, 3 ≤ 4 →1 ≤ 4.
よって半順序だと思うのですが、正解ですか？
もし正解ではなかったら、半順序の例を提示してくてると助かります
Re: ジャムさんへ
管理人 2023/07/23(Sun) 08:55 No.77
お疲れ様です。
HN変えてもIP同じなんでわかります。
貴方が頭がいいことは分かりますので、大学の内容に関しましては今後知恵袋でご質問ください。
よろしくお願い申し上げます。
HN変えてもIP同じなんでわかります。
貴方が頭がいいことは分かりますので、大学の内容に関しましては今後知恵袋でご質問ください。
よろしくお願い申し上げます。
管理人 2023/07/23(Sun) 08:55 No.77
命題
次の命題を簡略化したものがあっているかどうか確認したいです。
( P v ¬ Q ) →(P Λ Q)
答えは (P v Q) ∧ (¬P v Q)でしょうか？
解答手順は、
1.(P v ¬Q) → (P ∧ Q)
2.¬(P v ¬Q) ∨ (P ∧ Q)
3.(¬P ∧ Q) ∨ (P ∧ Q) (ドモルガン)
4.(¬P v P) ∧ (¬P v Q) ∧ (P v Q) (分配法則)
5.(¬P v Q) ∧ (P v Q) (べき等則)
6.(P v Q) ∧ (¬P v Q) (交換法則)
どうぞよろしくお願いします
( P v ¬ Q ) →(P Λ Q)
答えは (P v Q) ∧ (¬P v Q)でしょうか？
解答手順は、
1.(P v ¬Q) → (P ∧ Q)
2.¬(P v ¬Q) ∨ (P ∧ Q)
3.(¬P ∧ Q) ∨ (P ∧ Q) (ドモルガン)
4.(¬P v P) ∧ (¬P v Q) ∧ (P v Q) (分配法則)
5.(¬P v Q) ∧ (P v Q) (べき等則)
6.(P v Q) ∧ (¬P v Q) (交換法則)
どうぞよろしくお願いします
Re: 命題
管理人 2023/07/14(Fri) 17:26 No.74
そもそもの数学の記号が分かりませんので、
知恵袋で聞いてください。
私には手に負えません。
皆さん私より賢いですから。
それでは。
知恵袋で聞いてください。
私には手に負えません。
皆さん私より賢いですから。
それでは。
管理人 2023/07/14(Fri) 17:26 No.74
極限
非常に簡単な問題で恐縮ですが、以下の極限の問題の解き方がわかりません。ご解説お願いできますと幸いです。
(1) x→∞の時のlim(x+3/x+4)^(x+4)
(2)x→0の時のlim(√x+1 + √4x+2 + √9x+3)/x ※x+1、4x+2、9x+3がそれぞれルートの中に含まれる
よろしくお願いいたします。
(1) x→∞の時のlim(x+3/x+4)^(x+4)
(2)x→0の時のlim(√x+1 + √4x+2 + √9x+3)/x ※x+1、4x+2、9x+3がそれぞれルートの中に含まれる
よろしくお願いいたします。
Re: 極限
管理人 2023/07/11(Tue) 07:09 No.70
自信ないですがご参考までに。
画像をクリックしてご覧ください。
画像をクリックしてご覧ください。
管理人 2023/07/11(Tue) 07:09 No.70
Re: 極限
管理人様
丁寧な解説ありがとうございました。
大変勉強になりました。
丁寧な解説ありがとうございました。
大変勉強になりました。